Algorithms

`trueq.algorithms.algorithms.bernstein_vazirani`	Returns a circuit which implements the Bernstein-Vazirani algorithm for finding a hidden bitstring \(s \in \{0, 1\}^n\) that defines a function \(f: \{0, 1\}^n \rightarrow\{0, 1\}\) via \(f(x) = x_1 s_1 \oplus \dots \oplus x_n s_n\).
`trueq.algorithms.algorithms.simon`	Returns a circuit which implements Simon's algorithm for a periodic function \(f: \{0, 1\}^n \rightarrow \{0, 1\}^n\) specified by the period \(s \in \{0, 1\}^n\) via \(f(x) = x \oplus x_i s\), where \(i\) is the smallest index for which \(s_i = 1\).
`trueq.algorithms.subroutines.qft`	Returns a circuit which implements the quantum Fourier transform on \(n\)-qubits, \(\mathcal{F}_{2^n}\).

Algorithms

trueq.algorithms.algorithms.bernstein_vazirani(bitstring)

Returns a circuit which implements the Bernstein-Vazirani algorithm for finding a hidden bitstring \(s \in \{0, 1\}^n\) that defines a function \(f: \{0, 1\}^n \rightarrow\{0, 1\}\) via \(f(x) = x_1 s_1 \oplus \dots \oplus x_n s_n\). Classically one needs to evaluate the function \(f\) at least \(\Omega(n)\) times to achieve this task, whereas this quantum algorithm requires a single application of a unitary circuit satisfying \(U_f |x \rangle |b\rangle = |x \rangle |b\oplus f(x) \rangle\) for all \(x \in \{0,1\}^n\) and \(b \in \{0,1\}\).

import trueq as tq
import numpy as np

circuit = tq.algorithms.bernstein_vazirani((1, 1, 1, 1, 1))
circuit.draw()

# simulate the circuit and plot the output distribution
tq.Simulator().sample(circuit, n_shots=np.inf).plot()

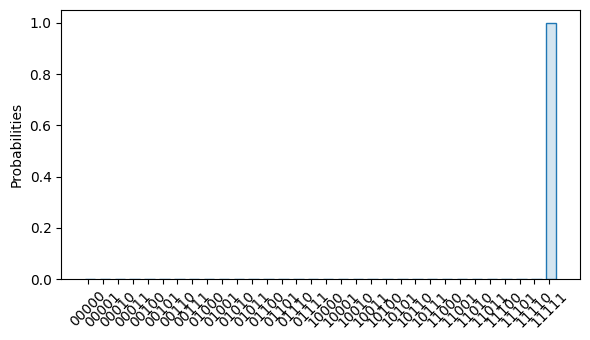
Parameters:: bitstring (tuple) – The bitstring that defines the function \(f\).
Return type:: Circuit

trueq.algorithms.algorithms.simon(period)

Returns a circuit which implements Simon’s algorithm for a periodic function \(f: \{0, 1\}^n \rightarrow \{0, 1\}^n\) specified by the period \(s \in \{0, 1\}^n\) via \(f(x) = x \oplus x_i s\), where \(i\) is the smallest index for which \(s_i = 1\).

Simon’s problem is to find the (hidden) period \(s\) given oracle access to a function \(f\) that satisfies the periodicity property: \(f(x) = f(y)\) if and only if \(x = y\) or \(x = y \oplus s\). Every probabilistic classical algorithm that solves this problem requires at least \(\Omega(2^{n/2})\) evaluations of the function \(f\), whereas Simon’s algorithm requires only \(O(n)\) calls to a unitary satisfying \(U_f |x \rangle |y\rangle = |x \rangle |y\oplus f(x) \rangle\).

The circuit uses \(n-1\) auxiliary qubits, and maps the \(n\)-qubit data register to a uniform superposition of all computational basis states \(|x\rangle\) that satisfy \(x_1 s_1 \oplus \dots \oplus x_n s_n = 0\). To compute the period \(s\) on the quantum computer, one draws \(O(n)\) samples from the output state, then uses classical processing to find \(s\) by solving a system of binary linear constraints.

import trueq as tq
import numpy as np

circuit = tq.algorithms.simon((1, 1, 1, 1, 1))
circuit.draw()

# simulate the circuit and plot the output distribution
tq.Simulator().sample(circuit, n_shots=np.inf).plot()

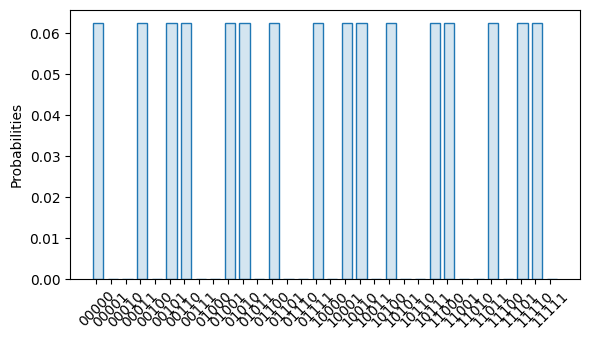
Parameters:: period (tuple) – The period of the implictly defined function \(f\).
Return type:: Circuit

Subroutines

trueq.algorithms.subroutines.qft(labels, truncate_at=None, swap=True)

Returns a circuit which implements the quantum Fourier transform on \(n\)-qubits, \(\mathcal{F}_{2^n}\).

By default, the returned circuit contains no approximations. However, by calling this method with an integer value for truncate_at, the returned circuit will be approximated by truncating certain controlled-\(Z\) rotations. Given an integer \(b\), the approximated Fourier transform will not contain controlled-\(Z\) rotations with angles smaller than \(2 \pi / 2^{b+1}\), or in other words, all cascades of controlled rotations will have depth no longer than \(b\).

Setting swap to False omits the final subcircuit which reverses the order of the qubits. This step requires \(O(n)\) swap gates, and can be safely omitted and replaced by classical post-processing if the QFT is immediately followed by measurement.

import numpy as np
import trueq as tq

circuit = tq.algorithms.qft(range(4), truncate_at=2)
circuit.measure_all()
circuit.draw()

Parameters:

labels (Iterable) – The qubit labels on which the Fourier transform acts.
truncate_at (NoneType | int) – An integer \(b\), which specifies the removal of all controlled-\(Z\) gates with an angle smaller than \(2 \pi / 2^b\), or None by default to remove no gates in the generated circuit.
swap (bool) – Whether to include the subcircuit which reverses the order of the qubits at the end of the QFT circuit. Default is True.

Return type:

Circuit