---

Download

Download this file as Jupyter notebook: simulator_advanced.ipynb.

Example: Advanced Simulator Usage

The Simulator can be configured with custom or pre-defined noise models. Noise models can define gate and cycle noise, as well as preparation and measurement noise.

Modeling Noise

A Simulator instance owns an ordered list of noise models, represented as NoiseSource objects. There are a number of built-in noise models, which can be added to the simulator via the add_*() wrapper functions, which are formatted such that they can be chained together in a single simulator instance as follows:

import numpy as np
import matplotlib.pyplot as plt

import trueq as tq
import trueq.simulation as tqs

# make a simulator that first over-rotates single qubit gates by 0.03, and then
# adds stochastic error in the X direction
sim = tq.Simulator().add_overrotation(0.03).add_stochastic_pauli(px=0.02)

These add_* functions create and append a noise source to the simulator, without requiring the direct use of NoiseSources. If desired, both built-in and custom defined noise sources can be appended to the simulator directly via append_noise_source(). An example of defining a custom noise source by extending NoiseSource and appending it to the simulator is provided at the end of this guide.

Built-in Noise Models

The Simulator supports a series of common noise models, such as:

1. add_depolarizing(): This method adds depolarizing noise to every location where a gate acts through application of a tensor product of local depolarizing channels. It takes the depolarizing parameter p as an argument.

2. add_stochastic_pauli(): This method adds stochastic Pauli noise to every location where a gate acts. It takes as parameters the probabilities of each Pauli error for the noise channel.

3. add_overrotation(): This method adds an overrotation to every single- and/or two-qubit gate. It takes as parameters the single_sys angle which specifies how much the single-qudit gates are under/overrotated, and the multi_sys parameter, which specifies how much the two-qudit gates are under/overrotated.

4. add_relaxation(): This method adds amplitude damping (\(T1\)) and/or dephasing (\(T2\)) to every location where a gate acts. This method takes as arguments the noise parameters t1 and t2 and the amount of time t_single (t_multi) a single- (multi-)qubit gate takes.

5. add_kraus(): This method allows for the creation of a custom noise source specified through Kraus operators and takes as input a list of operators specifed in matrix-form.

For a full list of built-in noise sources, check out the Simulator API reference.

General Noise Sources

A NoiseSource object contains two important features: a Match object as a property, and a method called apply(). This method takes as arguments the current cycle to simulate [1], the simulation backend (described below), and a cache of information that can optionally be used to store information about the circuit containing the cycle. The job of the apply method is to inform the simulation backend about all of the noise it wishes to apply. The noise can come in the form of Gates, Superops, state preparation errors, or measurement errors.

Conditional Noise

The Match class provides the ability to instruct noise sources to act on a filtered set of operations in each cycle. There are a variety of built-in matches, which allow matching noise sources to specific labels, gates, cycles, as well as matching to only single qubit gates, 90 degree rotations in the XY plane of the Bloch sphere, logical combinations of all of these, etc. Match objects are passed to built-in noise sources via the match argument, as the following example demonstrates:

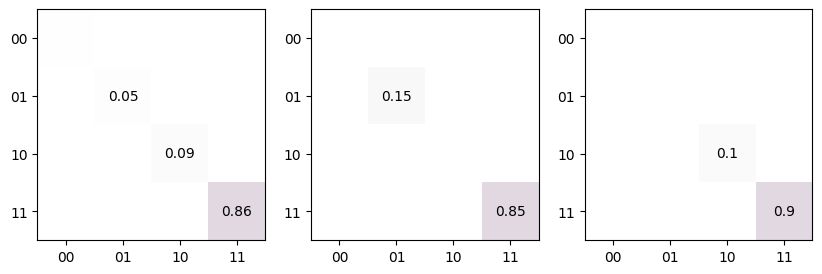
# create a sample circuit
circuit = tq.Circuit([{0: tq.Gate.x, 1: tq.Gate.y}, {(0, 1): tq.Gate.cz}])

# initialize a simulator with different dephasing rates on the qubits
bitflip = lambda p: [np.sqrt(1 - p) * np.eye(2), np.sqrt(p) * np.fliplr(np.eye(2))]
sim0 = tq.Simulator()
sim0.add_kraus(bitflip(0.05), match=tqs.LabelMatch(0))
sim0.add_kraus(bitflip(0.09), match=tqs.LabelMatch(1))

# initialize a simulator that targets only a specific gate
xmatch = tqs.GateMatch(tq.Gate.x)
sim1 = tq.Simulator().add_kraus(bitflip(0.15), match=xmatch)

# initialize a simulator that targets only specific gates on specific labels
sim2 = tq.Simulator()
gate_label_match = tqs.LabelMatch((1, 2)) & tqs.GateMatch([tq.Gate.y, tq.Gate.s])
sim2.add_kraus(bitflip(0.1), match=gate_label_match)

# plot the final states
plt.figure(figsize=(10, 3))
tq.plot_mat(sim0.state(circuit).mat(), ax=plt.subplot(131))
tq.plot_mat(sim1.state(circuit).mat(), ax=plt.subplot(132))
tq.plot_mat(sim2.state(circuit).mat(), ax=plt.subplot(133))

Simulation Backends

There are many strategies for performing a quantum simulation on a classical computer, and users can change the backend of a Simulator during construction.

Only advanced usage of the simulator requires an understanding of how simulation backends work, and what follows is a high level overview. The actual simulation of a quantum circuit is abstracted away from the Simulator and its noise sources into some implementation of the abstract SimulationBackend class.

A simulation backend contains a Runner class with methods like process_gate() and process_superop() which the noise sources invoke. After all noise sources have been run on all cycles in the circuit, one can access the final simulation via the simulation backend attribute value, though this is usually done automatically by the helper methods operator(), run(), sample(), or state().

The default simulation backend is PropagationBackend whose runner performs simulation by updating the value of one of the following objects, depending on the nature of the simulation at hand:

• A StateTensor which can store either a pure state or a mixed state. Anytime it represents a pure state and a noise model asks it to update by a non-unitary operation, it casts itself into a mixed state.

• A OperatorTensor which can store either a unitary or a superoperator. Anytime it represents a unitary and a noise model asks it to update itself by a non-unitary operation, it casts itself into a superoperator.

During the simulation of a circuit, the simulator iterates through cycles and passes each cycle (within the cycle wrapper class) to each noise model in turn [1] . The order of noise sources is defined by the order in which they are added to the simulator. Note that if none of the added noise sources attempt the simulation of a particular gate (e.g. all noise sources only add perturbations to the state based on the operations they see), then an ideal simulation of these missing gates automatically follows.

Advanced Note

The following note is included for advanced users of the simulator and for the benefit of users who are interested in writing their own noise model (an example is provided in the examples section).

Every simulator has a default noise source whose job is to attempt to simulate any previously un-simulated operations. This default noise source is automatically appended to a simulator’s noise sources during simulation. In order to ensure an operation is simulated only once, every noise source defines a flag that specifies whether it is the kind of noise source that tries to actually implement the operations it finds, as opposed to only injecting noise. For example, add_overrotation() sets this flag to True because it implements gates as \(U^{1+\epsilon}\) which is an attempt to actually implement \(U\), but add_depolarizing() sets this flag to False because it just adds a small perturbation to the state or superoperator during each cycle. During simulation each operator is temporarily wrapped in an OpWrapper whose purpose is to store this metadata via the attribute has_been_simulated.

For example, consider the following simulator:

sim = tq.Simulator().add_overrotation(single_sys=0.1, match=tqs.GateMatch(tq.Gate.x))

Here, every \(X\) operation encountered by the simulator will be overrotated, and will also be marked as has_been_simulated=True. Any other operations encountered by the simulator, such as a \(Z\) gate, will subsequently be simulated ideally.

Footnotes

[1] (1,2)

This description was slightly simplified for brevity. In order to allow non-Markovian noise, instead of accepting only the current cycle to simulate, apply() instead accepts a list of all cycles up to and including the current cycle. Markovian noise sources, which are the most common cases, will choose to only look at the current cycle.

---

Download

Download this file as Jupyter notebook: simulator_advanced.ipynb.