Randomized Compiling (RC)

See randomly_compile() for API documentation.

“I couldn’t imagine building a quantum computer without this.”

—John Martinis

Randomized compiling takes a circuit and randomizes its gates using virtual twirling groups while preserving the overall ideal unitary of the circuit [11]. This has the effect of converting coherent and non-Markovian error sources into stochastic errors, resulting in dramatically improved run-time performance and overall stability for quantum algorithms.

More concretely, randomized compiling inserts virtual random gates into a circuit and compiles them as shown in the figure below so that:

  1. The logical circuit is unchanged.

  2. The depth of the circuit is unchanged.

  3. The probability of obtaining a correct output for an algorithm run on noisy quantum hardware is significantly increased.

  4. The error prone quantum hardware can solve a given problem instance with greater accuracy and precision.

  5. The error prone quantum hardware can solve bigger problem instances with the same cumulative error budget.

  6. Algorithm output errors are more stable and predictable.

These improvements arise because coherent errors are suppressed (converted into stochastic errors) and many non-Markovian errors are decoupled. The main benefits of suppressing coherent and non-Markovian errors through randomized compiling include:

  1. Improved run-time performance and overall performance stability for quantum algorithms.

  2. Closing the gap between standard performance assessment data, as obtained via methods such as SRB and CB, and the predictable performance of quantum algorithms based on the assessment data.

These technical features imply the above performance improvements because of the following theoretical considerations. Norm-based quantities that quantify the impact of errors determine (i) the overall success probability with which noisy quantum hardware can execute a quantum algorithm of interest and (ii) the error threshold for fault-tolerance quantum error correction are both bounded by the diamond norm, defined by:

\[\epsilon_\diamond = ||\mathcal{E} - \mathcal{I}||_\diamond\]

The relationship between randomized benchmarking error rates and the diamond norm is very loose in the presence of coherent errors [12, 13] :

\[r(\mathcal{E})(1 + 2^{-N}) \leq \frac{1}{2}\epsilon_\diamond(\mathcal{E}) \leq 2^N \sqrt{r(\mathcal{E})}\sqrt{1 + 2^{-N}}\]

In particular, the exponential scaling with the number \(N\) of qubits and the \(\sqrt{r(\mathcal{E})}\) scaling is tight. Crucially, the \(\sqrt{r(\mathcal{E})}\) scaling increases reported error rates from \(10^{-6}\) to \(10^{-3}\). The diamond norm also bounds the increase in the TVD due to an error in a gate [14] for both worst-case and typical circuits.


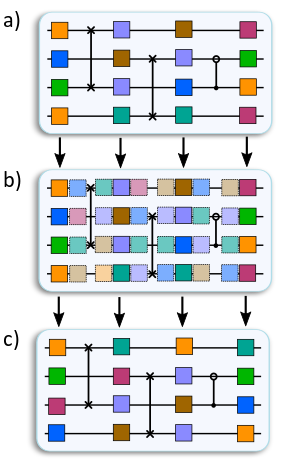
../../_images/circuit_diagram.png

Hard cycles of a bare input circuit (a) are surrounded by random twirling gates (b) that are compiled into existing easy cycles (c).

  • U.S. Patent 10,360,088 B2.

  • U.S. Patent 10,031,791 B2.