Download

Download this file as Jupyter notebook: synthesis.ipynb.

Example: Gate synthesis

This example demonstrates how the built-in compiler can be used to perform gate synthesis.

Synthesizing Single-Qubit Gates

We begin by generating a random gate in \(SU(2)\); we will synthesize this gate later.

[2]:

import trueq as tq

# create a Haar random SU(2) gate and print its matrix representation
U = tq.Gate.random(2)
U

[2]:
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".
Name:
  • Gate(Y, X, ...)
Generators:
  • 'Y': 130.189
  • 'X': 28.197
  • 'Z': -67.881
Matrix:
  • -0.41 0.31j 0.09 -0.85j 0.27 0.82j 0.46 0.22j

We can perform single qubit gate decomposition into a number of possible “modes”. Here we decompose the gate U into a ZXZXZ decomposition, which is short hand for \(Z(\theta)X(90)Z(\phi)X(90)Z(\gamma)\). See QubitMode for a complete list of all available single qubit decompositions.

[3]:

synthesized_gate = tq.math.QubitMode.ZXZXZ.decompose(U)

# print the synthesized gate as a list of single-qubit rotations about Z and X
synthesized_gate

[3]:

[('Z', -226.80129841701333),
 ('X', 90),
 ('Z', 61.45127515034275),
 ('X', 90),
 ('Z', -71.24264414521673)]

Synthesizing Two-Qubit Gates

In the event that we want to express a two-qubit gate in terms of a different two-qubit gate, we can use the compiler to synthesize the desired gate. Here we decompose a random \(SU(4)\) operation so that it can be implemented using iSWAP gates.

[4]:

# define the gate to be synthesized
gate_to_be_synthesized = tq.Gate.random(4)

# re-express the gate using an iswap gate as the two-qubit gate
two_qubit_synthesized_gate = tq.math.decompose_unitary(
    target_gate=gate_to_be_synthesized, given_gate=tq.Gate.iswap
)

# print the synthesized gate
two_qubit_synthesized_gate

[4]:
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".
Circuit
Key:
No key present in circuit.
 
Marker 0
Compilation tools may only recompile cycles with equal markers.
(0): Gate(Y, X, ...)
Name:
  • Gate(Y, X, ...)
Generators:
  • 'Y': 20.147
  • 'X': 3.942
  • 'Z': -61.301
Matrix:
  • -0.62 0.77j 0.05 -0.16j 0.01 0.17j 0.39 0.91j
(1): Gate(Y, X, ...)
Name:
  • Gate(Y, X, ...)
Generators:
  • 'Y': 20.897
  • 'X': -129.81
  • 'Z': 30.426
Matrix:
  • 0.08 -0.43j 0.60 0.67j 0.78 0.45j 0.40 -0.17j
 
Marker 0
Compilation tools may only recompile cycles with equal markers.
(0, 1): Gate.iswap
Name:
  • Gate.iswap
Aliases:
  • Gate.iswap
Likeness:
  • iSWAP
Generators:
  • 'YY': -90.0
  • 'XX': -90.0
Matrix:
  • 1.00 1.00j 1.00j 1.00
 
 
Marker 0
Compilation tools may only recompile cycles with equal markers.
(0): Gate(Y, X, ...)
Name:
  • Gate(Y, X, ...)
Generators:
  • 'Y': 84.323
  • 'X': 125.095
  • 'Z': -94.09
Matrix:
  • -0.45 0.28j 0.37 -0.76j 0.85 0.06j 0.47 -0.25j
(1): Gate(Y, X, ...)
Name:
  • Gate(Y, X, ...)
Generators:
  • 'Y': -113.407
  • 'X': -87.354
  • 'Z': -12.891
Matrix:
  • 0.20 -0.25j 0.83 -0.45j 0.23 0.92j 0.05 -0.32j
 
Marker 0
Compilation tools may only recompile cycles with equal markers.
(0, 1): Gate.iswap
Name:
  • Gate.iswap
Aliases:
  • Gate.iswap
Likeness:
  • iSWAP
Generators:
  • 'YY': -90.0
  • 'XX': -90.0
Matrix:
  • 1.00 1.00j 1.00j 1.00
 
 
Marker 0
Compilation tools may only recompile cycles with equal markers.
(0): Gate(Y, X, ...)
Name:
  • Gate(Y, X, ...)
Generators:
  • 'Y': 149.084
  • 'X': 20.377
  • 'Z': -66.048
Matrix:
  • -0.13 0.40j -0.64 -0.64j 0.79 0.44j 0.35 -0.24j
(1): Gate(Y, X, ...)
Name:
  • Gate(Y, X, ...)
Generators:
  • 'Y': -114.85
  • 'X': 161.747
  • 'Z': 159.579
Matrix:
  • -0.33 -0.71j 0.54 -0.30j -0.10 -0.61j -0.76 0.18j
 
Marker 0
Compilation tools may only recompile cycles with equal markers.
(0, 1): Gate.iswap
Name:
  • Gate.iswap
Aliases:
  • Gate.iswap
Likeness:
  • iSWAP
Generators:
  • 'YY': -90.0
  • 'XX': -90.0
Matrix:
  • 1.00 1.00j 1.00j 1.00
 
 
Marker 0
Compilation tools may only recompile cycles with equal markers.
(0): Gate(Y, X, ...)
Name:
  • Gate(Y, X, ...)
Generators:
  • 'Y': 32.227
  • 'X': -193.873
  • 'Z': -26.455
Matrix:
  • -0.20 0.04j -0.59 0.78j -0.30 0.93j -0.08 -0.19j
(1): Gate(Y, X, ...)
Name:
  • Gate(Y, X, ...)
Generators:
  • 'Y': 88.663
  • 'X': -2.655
  • 'Z': 70.089
Matrix:
  • 0.71 -0.26j -0.61 -0.24j 0.60 0.27j 0.31 0.69j

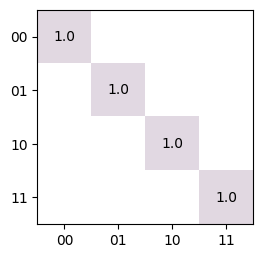
This circuit can be verified to reproduce the original random unitary using an ideal simulator:

[5]:

matrix = tq.Simulator().operator(two_qubit_synthesized_gate).mat()

# This will result in an identity gate up to a global complex phase.
tq.plot_mat(matrix @ gate_to_be_synthesized.adj.mat)
../../_images/guides_compilation_synthesis_8_0.png

Download

Download this file as Jupyter notebook: synthesis.ipynb.