---

Download

Download this file as Jupyter notebook: cb_example.ipynb.

Example: Running CB

This example explores the Cycle Benchmarking (CB) protocol that allows us to characterize the process infidelity of a dressed cycle (a target cycle preceded by a cycle of random elements of the twirling group).

Choosing Parameters

The make_cb() method generates a circuit collection to perform cycle benchmarking. The first argument required by make_cb() is the cycle to be benchmarked. The second parameter n_random_cycles is also a required parameter, it tells make_cb() how many times to apply the dressed cycle in each random circuit.

The number of circuits for each circuit length, n_circuits, is 30 by default and should be chosen to optimize the tradeoff between desired speed and accuracy of the estimation.

The number of randomly chosen Pauli decay strings used to measure the process fidelity, n_decays, should be chosen to exceed \(min(20, 4^{n_{qubits}} - 1)\). The default value for n_decays is 20 to satisfy this bound. Choosing a value lower than \(min(20, 4^{n_{qubits}} - 1)\) may result in a biased estimate of the fidelity of the dressed cycle.

The twirl parameter specifies which twirling group the random gates which form the pre-compiled dressed cycles are pulled from. By default, make_cb() uses the Pauli group, "P".

The choice of circuit lengths in n_random_cycles depends on the cycle being characterized as well as the selection of twirling group. If the cycle is a Clifford and the twirling group is "P", lengths should be chosen such that applying the cycle to be benchmarked n_random_cycles times will result in an identity operation. In the example below, we benchmark a cycle containing an \(X\) gate and a controlled-\(Z\) gate, both of which apply an identity operation when raised to even powers. We therefore choose cycle lengths 4, 12, 24. While the values of n_random_cycles can be any multiple of 2 for this example, users should be careful to choose a range of values such that the exponential decay is evident in the plot; this will ensure that the fit function gets enough information to accurately estimate the fidelity of the dressed cycle. To validate that this condition has been satisfied, users can plot the data from the CB circuits after running the circuits on a simulator or on hardware to see where the chosen data points fall.

The final parameter is a bool, propagate_correction, which tells make_cb() whether to compile correction gates for the twirling group into neighbouring cycles (propagate_correction=False) or propagate them to the end of the circuit (propagate_correction=True). By default, propagate_correction=False. Warning: propagating correction to the end of the circuit can result in arbitrary two-qubit gates at the end of the circuit! The final circuit can be converted to a user-specified gateset using the Compilation Tools tools.

Benchmarking a Cycle

We begin by initializing a cycle to benchmark:

import trueq as tq

cycle = {(0,): tq.Gate.x, (1, 2): tq.Gate.cz}

Generate a circuit collection to run CB on the above cycle with n_circuits=30 random circuits for each circuit length in n_random_cycles=[4, 12, 24] and n_decays=24 randomly chosen Pauli decay strings. For the purpose of demonstrating how to recognize a poor choice of n_random_cycles, we generate a second CB circuit collection with the same parameters, except n_random_cycles=[2, 4, 6]. A good choice of n_random_cycles will result in a lower uncertainty in the fit parameters and therefore a more accurate estimate of the average gate fidelity.

circuits = tq.make_cb(cycle, [4, 12, 24], 30, 24)
bad_circuits = tq.make_cb(cycle, [2, 4, 6], 30, 6)

Initialize a simulator with stochastic Pauli noise and run the cycle benchmarking circuits on the simulator to populate their results. Given this error model, we expect the individual Pauli infidelities corresponding to strings with more than two \(Z\) or \(Y\) to be \(0.01 \times 2 \times\) # of \(Z/X\) terms, where the factor of two comes from simulating errors in both the random and interleaved cycles.

sim = tq.Simulator().add_stochastic_pauli(px=0.01)
sim.run(circuits)
sim.run(bad_circuits)

Plot the results of the circuits with badly chosen n_random_cycles:

bad_circuits.plot.raw()

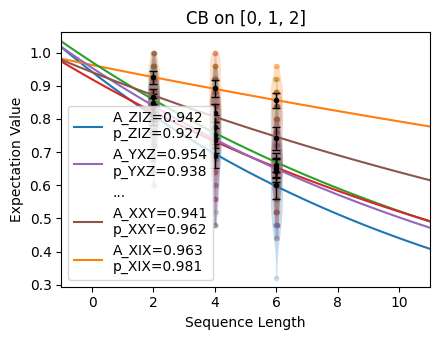
We can see in the plots above that our choices of n_random_cycles are sampling from the nearly linear portion of the exponential decay. While this is valid, it is not efficient (in terms of the amount of required data) at precisely learning the decay rates. Below, we show the same plots for the better choice n_random_cycles=[4, 12, 24] (ideally, the best place to sample is \(1/e\approx 0.37\)).

circuits.plot.raw()

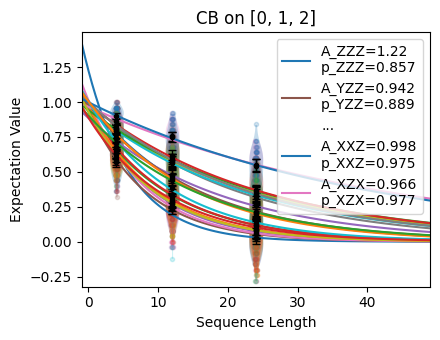
The output parameters of this protocol are displayed below using the fit() function. When the circuits were generated, n_decays=24 random three-qubit Paulis were chosen as representatives, and the rate of decay of each was measured; these decay rates are reported. However, the parameter of interest is the composite parameter e_F, which is an estimate of the process infidelity of the entire cycle.

circuits.fit()

True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".

CB Cycle Benchmarking	Paulis (0,) : Gate.x (1, 2) : Gate.cz Key: cycles: (Cycle((0,): Gate.x, (1, 2): Gate.cz),) labels: (0, 1, 2) protocol: CB twirl: Paulis on [0, 1, 2]
${e}_{F}$ The probability of an error acting on the specified labels during a dressed cycle of interest.	7.0e-02 (5.2e-03) 0.07004009292219604, 0.005224644061859647
${e}_{III}$ The probability of the subscripted error acting on the specified labels.	9.3e-01 (5.2e-03) 0.929959907077804, 0.005224644061859647
${p}_{ZZZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.6e-01 (3.5e-02) 0.8572524724864501, 0.035151066005922445
${p}_{ZZY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.0e-01 (1.9e-02) 0.9041630554501853, 0.019101509499363116
${p}_{ZYZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.0e-01 (1.7e-02) 0.9046384125229662, 0.016673914415200244
${p}_{ZYY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.2e-01 (9.3e-03) 0.9172649669378943, 0.009282671746887756
${p}_{ZYX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.2e-01 (8.3e-03) 0.9178200864723023, 0.008271529140448054
${p}_{ZYI}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.0e-01 (9.7e-03) 0.8986747898147458, 0.00968493653037383
${p}_{ZIZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.2e-01 (6.6e-03) 0.9207877274139996, 0.0066279573217489654
${p}_{ZIY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.9e-01 (1.4e-02) 0.8896976028684801, 0.01440120272976041
${p}_{YZZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.9e-01 (2.2e-02) 0.8887585808198403, 0.021854136874028145
${p}_{YZY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.1e-01 (1.3e-02) 0.9142224995396199, 0.013210367810893957
${p}_{YZX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (6.7e-03) 0.9413616926443233, 0.006662072023703954
${p}_{YYZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.0e-01 (1.8e-02) 0.9032161844934384, 0.017588237682121165
${p}_{YXI}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01 (4.5e-03) 0.9495085056136472, 0.00453856205208943
${p}_{YIX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (4.3e-03) 0.9389473153208007, 0.004300847634303788
${p}_{XZX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01 (2.3e-03) 0.9770098626296241, 0.002317154902601905
${p}_{XZI}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01 (3.8e-03) 0.9532449400874499, 0.0038028543928984183
${p}_{XYX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (4.1e-03) 0.9596370794946087, 0.004104855147224384
${p}_{XYI}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (6.7e-03) 0.9353380050050057, 0.00666793871670377
${p}_{XXZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01 (2.2e-03) 0.9754096176680155, 0.0021697203289248006
${p}_{XXY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (3.8e-03) 0.9575506795168859, 0.0038270109340705592
${p}_{IYY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (3.0e-03) 0.9611878405006208, 0.0029599626001712573
${p}_{IXX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (4.7e-03) 0.9567738600503727, 0.004741126918604711
${p}_{IIZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (1.5e-03) 0.9599354074632576, 0.0015473370054274313
${p}_{IIY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (3.1e-03) 0.9366365850527654, 0.003066733930085238
${A}_{ZZZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.2e+00 (3.6e-01) 1.2237925695548877, 0.35610676739690617
${A}_{ZZY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.3e-01 (1.4e-01) 0.9309778599235778, 0.1439318967907059
${A}_{ZYZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (1.3e-01) 0.9626648702998909, 0.13312750841730667
${A}_{ZYY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01 (7.5e-02) 0.9505669468392534, 0.07461025464618122
${A}_{ZYX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.3e-01 (6.6e-02) 0.9290660355621322, 0.06597250772360566
${A}_{ZYI}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01 (7.8e-02) 0.9750520484065625, 0.07834592020819117
${A}_{ZIZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (5.7e-02) 1.001640480661014, 0.057309707570599264
${A}_{ZIY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (1.2e-01) 1.0118411393458793, 0.11967972175131687
${A}_{YZZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (1.7e-01) 0.9423012350940094, 0.16833603022182636
${A}_{YZY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.9e-01 (9.8e-02) 0.887187869718767, 0.0975003011665624
${A}_{YZX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.0e-01 (5.5e-02) 0.9020379025483662, 0.05492412511932285
${A}_{YYZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.7e-01 (1.4e-01) 0.9710656358177482, 0.13876656308261037
${A}_{YXI}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.9e-01 (4.0e-02) 0.8850266111072104, 0.040256840769439174
${A}_{YIX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01 (3.7e-02) 0.9810534867699633, 0.03721180116354824
${A}_{XZX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.7e-01 (2.2e-02) 0.9655337054525753, 0.02175971691415384
${A}_{XZI}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (3.5e-02) 1.0032839768283828, 0.03547755094456757
${A}_{XYX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (3.6e-02) 0.9416761451820955, 0.03608629665559626
${A}_{XYI}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (5.7e-02) 1.0046720046484676, 0.057431413862642326
${A}_{XXZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (2.1e-02) 0.9983665823647017, 0.021467885377639117
${A}_{XXY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (3.7e-02) 0.9448690589939369, 0.036925817251788756
${A}_{IYY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (2.8e-02) 0.9418311988447358, 0.027978009497041465
${A}_{IXX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.9e-01 (4.1e-02) 0.9943968896085044, 0.04098821909341424
${A}_{IIZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.9e-01 (1.5e-02) 0.985956810820951, 0.014622886330565401
${A}_{IIY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (2.7e-02) 1.0072085927367365, 0.02701337103264106

The default fit is to the process infidelity of the entire dressed cycle. We can also manually specify qubit labels to query the process infidelity of subsets of qubits, whose errors will be with respect to the context of the entire cycle.

circuits.fit(labels=[0, [1, 2], [0, 1, 2]]).plot.compare_twirl("e_F")

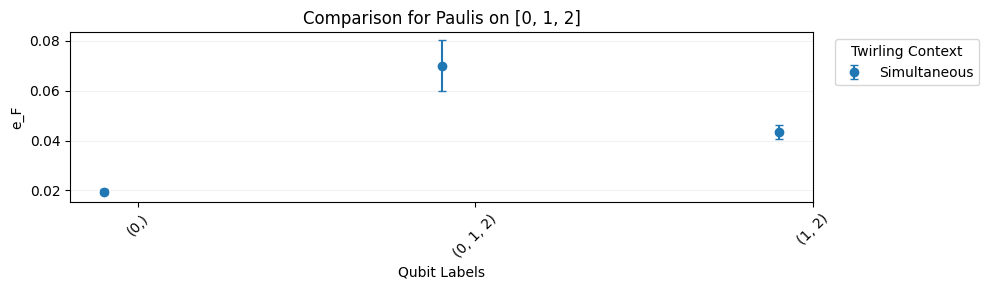
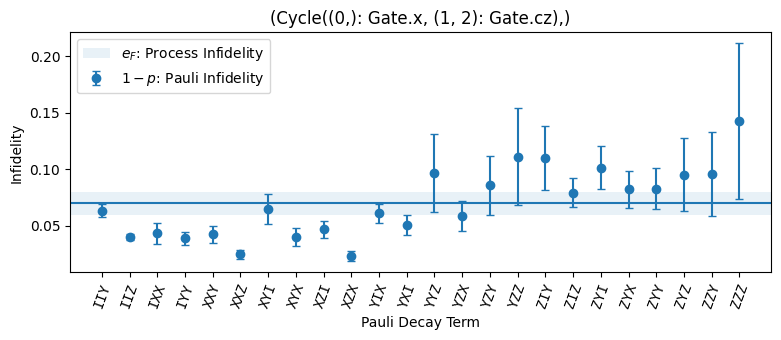
Finally, we can compare the individual Pauli infidelities (see CB for definitions), whose average value estimates the process infidelity. See also stochastic calibration SC to select these curves manually.

circuits.plot.compare_pauli_infidelities()

Targeting Specific Errors

We can also use cycle benchmarking to estimate the probabilities of specific errors. These errors can be supplied using an optional parameter targeted_errors at generation (see make_cb() for more details) or by updating the keys of existing CB circuits. We demonstrate the latter approach below. Note that if your circuits are already populated with results, the length of each error must correspond to the number of measurements in your circuits.

targets = tq.math.Weyls("XII_ZII_IIX_IIZ")
circuits.update_keys(targeted_errors=targets)
circuits.fit()

True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".

CB Cycle Benchmarking	Paulis (0,) : Gate.x (1, 2) : Gate.cz Key: cycles: (Cycle((0,): Gate.x, (1, 2): Gate.cz),) labels: (0, 1, 2) protocol: CB twirl: Paulis on [0, 1, 2]
${e}_{F}$ The probability of an error acting on the specified labels during a dressed cycle of interest.	7.0e-02 (5.2e-03) 0.07004009292219604, 0.005224644061859647
${e}_{ZII}$ The probability of the subscripted error acting on the specified labels.	-1.1e-02 (5.0e-03) -0.011223839824967385, 0.004995883375437728
${e}_{XII}$ The probability of the subscripted error acting on the specified labels.	2.3e-02 (3.3e-03) 0.02341069771633414, 0.003342780578849372
${e}_{IIZ}$ The probability of the subscripted error acting on the specified labels.	-6.9e-03 (5.4e-03) -0.00694777631891158, 0.00541441014311624
${e}_{IIX}$ The probability of the subscripted error acting on the specified labels.	1.1e-02 (4.7e-03) 0.011032891401843326, 0.0046981708878685085
${e}_{III}$ The probability of the subscripted error acting on the specified labels.	9.3e-01 (5.2e-03) 0.929959907077804, 0.005224644061859647
${p}_{ZZZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.6e-01 (3.5e-02) 0.8572524724864501, 0.035151066005922445
${p}_{ZZY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.0e-01 (1.9e-02) 0.9041630554501853, 0.019101509499363116
${p}_{ZYZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.0e-01 (1.7e-02) 0.9046384125229662, 0.016673914415200244
${p}_{ZYY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.2e-01 (9.3e-03) 0.9172649669378943, 0.009282671746887756
${p}_{ZYX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.2e-01 (8.3e-03) 0.9178200864723023, 0.008271529140448054
${p}_{ZYI}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.0e-01 (9.7e-03) 0.8986747898147458, 0.00968493653037383
${p}_{ZIZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.2e-01 (6.6e-03) 0.9207877274139996, 0.0066279573217489654
${p}_{ZIY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.9e-01 (1.4e-02) 0.8896976028684801, 0.01440120272976041
${p}_{YZZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.9e-01 (2.2e-02) 0.8887585808198403, 0.021854136874028145
${p}_{YZY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.1e-01 (1.3e-02) 0.9142224995396199, 0.013210367810893957
${p}_{YZX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (6.7e-03) 0.9413616926443233, 0.006662072023703954
${p}_{YYZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.0e-01 (1.8e-02) 0.9032161844934384, 0.017588237682121165
${p}_{YXI}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01 (4.5e-03) 0.9495085056136472, 0.00453856205208943
${p}_{YIX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (4.3e-03) 0.9389473153208007, 0.004300847634303788
${p}_{XZX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01 (2.3e-03) 0.9770098626296241, 0.002317154902601905
${p}_{XZI}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01 (3.8e-03) 0.9532449400874499, 0.0038028543928984183
${p}_{XYX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (4.1e-03) 0.9596370794946087, 0.004104855147224384
${p}_{XYI}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (6.7e-03) 0.9353380050050057, 0.00666793871670377
${p}_{XXZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01 (2.2e-03) 0.9754096176680155, 0.0021697203289248006
${p}_{XXY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (3.8e-03) 0.9575506795168859, 0.0038270109340705592
${p}_{IYY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (3.0e-03) 0.9611878405006208, 0.0029599626001712573
${p}_{IXX}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (4.7e-03) 0.9567738600503727, 0.004741126918604711
${p}_{IIZ}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (1.5e-03) 0.9599354074632576, 0.0015473370054274313
${p}_{IIY}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (3.1e-03) 0.9366365850527654, 0.003066733930085238
${A}_{ZZZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.2e+00 (3.6e-01) 1.2237925695548877, 0.35610676739690617
${A}_{ZZY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.3e-01 (1.4e-01) 0.9309778599235778, 0.1439318967907059
${A}_{ZYZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01 (1.3e-01) 0.9626648702998909, 0.13312750841730667
${A}_{ZYY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01 (7.5e-02) 0.9505669468392534, 0.07461025464618122
${A}_{ZYX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.3e-01 (6.6e-02) 0.9290660355621322, 0.06597250772360566
${A}_{ZYI}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01 (7.8e-02) 0.9750520484065625, 0.07834592020819117
${A}_{ZIZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (5.7e-02) 1.001640480661014, 0.057309707570599264
${A}_{ZIY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (1.2e-01) 1.0118411393458793, 0.11967972175131687
${A}_{YZZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (1.7e-01) 0.9423012350940094, 0.16833603022182636
${A}_{YZY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.9e-01 (9.8e-02) 0.887187869718767, 0.0975003011665624
${A}_{YZX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.0e-01 (5.5e-02) 0.9020379025483662, 0.05492412511932285
${A}_{YYZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.7e-01 (1.4e-01) 0.9710656358177482, 0.13876656308261037
${A}_{YXI}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.9e-01 (4.0e-02) 0.8850266111072104, 0.040256840769439174
${A}_{YIX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01 (3.7e-02) 0.9810534867699633, 0.03721180116354824
${A}_{XZX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.7e-01 (2.2e-02) 0.9655337054525753, 0.02175971691415384
${A}_{XZI}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (3.5e-02) 1.0032839768283828, 0.03547755094456757
${A}_{XYX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (3.6e-02) 0.9416761451820955, 0.03608629665559626
${A}_{XYI}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (5.7e-02) 1.0046720046484676, 0.057431413862642326
${A}_{XXZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (2.1e-02) 0.9983665823647017, 0.021467885377639117
${A}_{XXY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (3.7e-02) 0.9448690589939369, 0.036925817251788756
${A}_{IYY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01 (2.8e-02) 0.9418311988447358, 0.027978009497041465
${A}_{IXX}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.9e-01 (4.1e-02) 0.9943968896085044, 0.04098821909341424
${A}_{IIZ}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.9e-01 (1.5e-02) 0.985956810820951, 0.014622886330565401
${A}_{IIY}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00 (2.7e-02) 1.0072085927367365, 0.02701337103264106

We can plot the probability of specific errors acting on the qubits during the cycle of interest:

circuits.plot.compare_twirl([f"e_{targ}" for targ in targets])

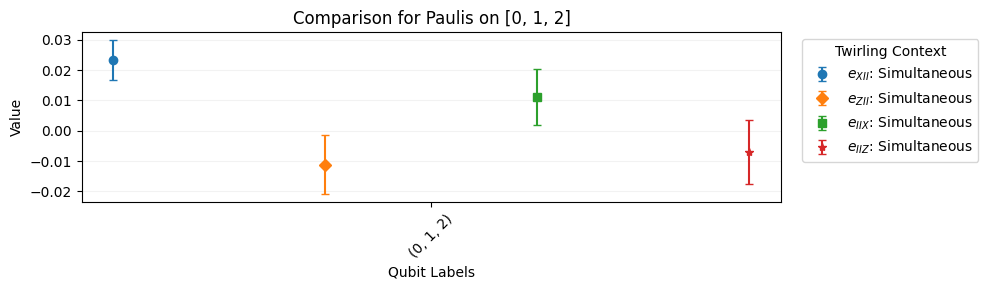
Cycle Benchmarking on Qudits

The make_cb() function natively extends to higher-dimensional qudits without any modifications, however when it comes to our choice of parameters we need to take the qudit dimension into account.

For this example, let’s consider a three-qutrit system and a single cycle consisting of a qutrit \(X\) gate and a controlled-\(Z\) gate (analogous to the qubit example above):

tq.settings.set_dim(3)

cycle = {(0,): tq.Gate.x3, (1, 2): tq.Gate.cz3}

# display the cycle in a circuit
tq.Circuit(cycle).draw()

To create the CB circuits, we need to modify our selected values to n_random_cycles such that all inputs are divisible by \(3\), since the \(CZ3\) gate used in our cycle is of order \(3\) (note that while the \(X3\) gate also has order \(3\), it leaves the Weyl Transfer Matrix invariant up to a phase and hence does not impose a restriction on the sequence length):

circuits = tq.make_cb(cycle, [3, 12, 24], 30, 24)

As before, we instantiate a simulator with a stochastic \(X\) error, but since we are now considering qudits, we implement a stochastic Weyl instead of Pauli error by calling the add_stochastic_weyl() method:

sim = tq.Simulator().add_stochastic_weyl(W10=0.01)
sim.run(circuits)

Note

Weyl operators are the generalization of the Pauli operators for higher qudit dimensions. Technically, the add_stochastic_weyl() and add_stochastic_pauli() methods for the Simulator are aliases of each other and implement the same operation, however we chose to use the add_stochastic_weyl() just to be explicit. See also Advanced Qudit Framework for more information on the mathematical background of Weyl operators.

When we plot the resulting decays, we expect to see both a real and imaginary component of the fit parameters because the stochastic Weyl error channel for dimensions larger than \(2\) has complex eigenvalues:

circuits.plot.raw()

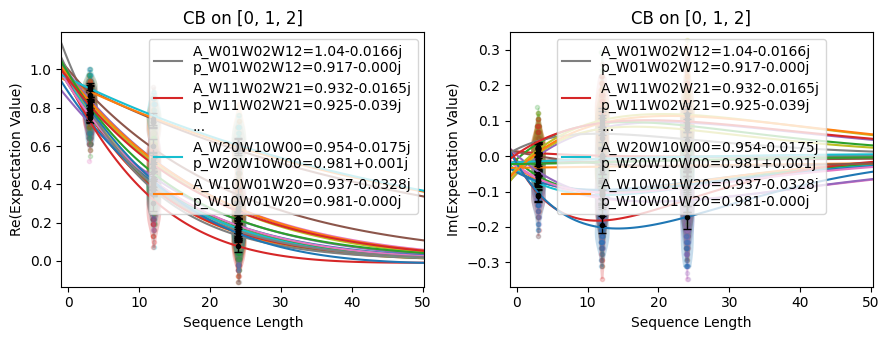
Note that the decay parameters are now expressed in terms of Weyl operators instead of Paulis.

And as before, we can inspect all fitted parameters by calling the fit() method:

circuits.fit()

True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".

CB Cycle Benchmarking	Paulis (0,) : Gate.x3 (1, 2) : Gate.cz3 Key: cycles: (Cycle((0,): Gate.x3, (1, 2): Gate.cz3),) labels: (0, 1, 2) protocol: CB twirl: Paulis on [0, 1, 2]
${e}_{F}$ The probability of an error acting on the specified labels during a dressed cycle of interest.	5.6e-02-0.0e+00j (4.9e-03) (0.056049740760708566-0j), 0.00485289503256181
${e}_{W00W00W00}$ The probability of the subscripted error acting on the specified labels.	9.4e-01+0.0e+00j (4.9e-03) (0.9439502592392914+0j), 0.00485289503256181
${p}_{W22W20W22}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.3e-01+1.8e-02j (6.9e-03) (0.9329886774170104+0.018360594183908792j), 0.006854841996365098
${p}_{W22W12W11}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01+1.8e-02j (5.7e-03) (0.9381238180950169+0.01781554598703514j), 0.005730128124772712
${p}_{W22W11W10}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.3e-01+1.1e-02j (6.8e-03) (0.9276980374126383+0.010712850456766716j), 0.006784344690092841
${p}_{W21W22W12}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01-1.4e-02j (6.4e-03) (0.9398897455357179-0.01421510699472264j), 0.006412987247396632
${p}_{W21W12W21}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01-1.7e-02j (6.6e-03) (0.9351139497758688-0.017184150504055716j), 0.006566533700969661
${p}_{W21W01W00}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01-3.4e-02j (5.4e-03) (0.940345666148192-0.03355009658531377j), 0.005422267376617773
${p}_{W20W12W02}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01+1.8e-02j (4.0e-03) (0.949933626492043+0.01833577828889067j), 0.003963148087313608
${p}_{W20W10W00}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01+6.4e-04j (1.6e-03) (0.9810910844654893+0.0006354907212936715j), 0.0015974375673026462
${p}_{W12W20W02}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01+1.4e-02j (4.2e-03) (0.9497720895209986+0.01411436360534217j), 0.0041659374197815045
${p}_{W11W11W12}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01-1.6e-02j (5.8e-03) (0.9388770595156465-0.01629312510298171j), 0.005837584974819043
${p}_{W11W02W21}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.2e-01-3.9e-02j (7.1e-03) (0.9245100141016572-0.038620229376452576j), 0.0070985765984242525
${p}_{W10W11W00}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01-1.6e-02j (3.9e-03) (0.953813611252825-0.015804053161001103j), 0.0039173481117884944
${p}_{W10W01W20}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01-4.0e-04j (1.9e-03) (0.9812003908172329-0.00040434133624270074j), 0.0018900627973834595
${p}_{W10W01W10}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01-2.8e-05j (1.8e-03) (0.9795284392908304-2.7838548172277942e-05j), 0.001763047584854601
${p}_{W02W21W21}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01+1.9e-02j (4.1e-03) (0.947485841655951+0.018831654710887775j), 0.004095157107319059
${p}_{W02W02W20}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01+1.7e-02j (4.1e-03) (0.9516347315404182+0.01715960350070863j), 0.004063694693834375
${p}_{W02W00W21}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.2e-01-7.9e-04j (4.7e-03) (0.9246865072827215-0.000790766364100958j), 0.004650173701735206
${p}_{W01W22W21}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.3e-01-1.9e-02j (7.8e-03) (0.9316111514709152-0.018688033946613152j), 0.0077625649052555255
${p}_{W01W12W22}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.3e-01-1.4e-02j (5.7e-03) (0.9333171583817003-0.014394123452667424j), 0.005677450152521261
${p}_{W01W10W10}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.3e-01-1.8e-02j (7.0e-03) (0.9288802207710757-0.017552897258055773j), 0.007037949927838243
${p}_{W01W02W12}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.2e-01-2.5e-04j (8.2e-03) (0.9173130684044493-0.00024825514222077483j), 0.008211767476455684
${p}_{W00W11W10}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01-3.9e-03j (3.9e-03) (0.9567130857382478-0.0038618862621849987j), 0.0038867303572389603
${p}_{W00W11W00}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01-1.7e-02j (1.7e-03) (0.951662688598027-0.01723707862678923j), 0.0017433983924145966
${p}_{W00W01W02}$ Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01-1.2e-03j (5.9e-03) (0.9386155580583173-0.0011607061611736609j), 0.0059171635200705374
${A}_{W22W20W22}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01-4.8e-02j (5.2e-02) (0.9601249915937368-0.04835831627506818j), 0.051584294856962705
${A}_{W22W12W11}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.2e-01-9.1e-03j (4.3e-02) (0.9204724070784503-0.009062249383710448j), 0.04342784994541727
${A}_{W22W11W10}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.9e-01+2.0e-02j (5.2e-02) (0.98531430803667+0.019728483348721283j), 0.05219936162449876
${A}_{W21W22W12}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.8e-01-4.6e-02j (4.7e-02) (0.8814935251723358-0.04563326358090577j), 0.04673762495957015
${A}_{W21W12W21}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01-4.1e-02j (5.2e-02) (0.9400771002477902-0.040846671522123644j), 0.05224312367113614
${A}_{W21W01W00}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01-2.0e-02j (4.4e-02) (0.96363201276077-0.020362413694421606j), 0.043570282339886364
${A}_{W20W12W02}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.7e-01-3.5e-02j (3.2e-02) (0.9654866052045782-0.035258035003161485j), 0.03155462781303916
${A}_{W20W10W00}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01-1.8e-02j (1.6e-02) (0.9541308783786987-0.017536429984779136j), 0.01641465209616356
${A}_{W12W20W02}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01+5.6e-03j (3.3e-02) (0.9496827009713168+0.005596020900512167j), 0.03283022081603062
${A}_{W11W11W12}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.2e-01-2.9e-02j (4.6e-02) (0.9203099546123451-0.02879438284561096j), 0.04565204346998111
${A}_{W11W02W21}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.3e-01-1.7e-02j (5.5e-02) (0.9320045802940097-0.01653502793650803j), 0.05515929883053845
${A}_{W10W11W00}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.3e-01-2.6e-02j (3.4e-02) (0.9341101798026737-0.026104350219234174j), 0.033737391054037634
${A}_{W10W01W20}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.4e-01-3.3e-02j (1.7e-02) (0.9371215541718817-0.03278027639114195j), 0.01710886677183053
${A}_{W10W01W10}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01-1.9e-02j (1.7e-02) (0.9484706943124778-0.019115724016001208j), 0.017079522540186156
${A}_{W02W21W21}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	8.5e-01-5.0e-02j (3.3e-02) (0.8456964288119742-0.049707687451437284j), 0.03346672218242478
${A}_{W02W02W20}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.7e-01-4.0e-02j (3.4e-02) (0.9681062075676168-0.040167844596232405j), 0.034423580499360056
${A}_{W02W00W21}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.7e-01+1.3e-02j (3.5e-02) (0.9697245407215616+0.013384562265949676j), 0.03513201119127715
${A}_{W01W22W21}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01-1.2e-02j (5.7e-02) (0.9472153185431812-0.012432122214787695j), 0.05697686978086869
${A}_{W01W12W22}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.6e-01-4.2e-02j (4.7e-02) (0.9560589194203803-0.04190722291113897j), 0.04677732557615107
${A}_{W01W10W10}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.5e-01-3.0e-02j (5.3e-02) (0.9517487935513218-0.029550308764882228j), 0.052975773482003864
${A}_{W01W02W12}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00-1.7e-02j (6.7e-02) (1.0439291838840628-0.016584813359975477j), 0.06705692565631201
${A}_{W00W11W10}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	1.0e+00+1.2e-02j (3.2e-02) (0.9988899365352669+0.012384608093651172j), 0.032330492222542175
${A}_{W00W11W00}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01+3.3e-03j (1.5e-02) (0.9810221880775524+0.0033304943746464972j), 0.014820088737271427
${A}_{W00W01W02}$ SPAM parameter of the exponential decay $Ap^m$ for the given Pauli term.	9.8e-01-2.2e-02j (4.8e-02) (0.9792989476145039-0.02222008867077291j), 0.0481418476155415

---

Download

Download this file as Jupyter notebook: cb_example.ipynb.