Download
Download this file as Jupyter notebook: srb_xrb_example.ipynb.
Example: Comparing Infidelities with SRB and XRB
This example demonstrates how to estimate the process infidelities of specified
systems using SRB, and how this quantity can be divided into coherent and
stochastic infidelity by the addition of XRB circuits. While this example
uses the built-in Simulator to execute the circuits, the same
procedure can be followed for hardware applications.
[2]:
import trueq as tq
# generate SRB circuits to simultaneously characterize a single qubit [0],
# a pair of qubits [1, 2], and another single qubit [3]
circuits = tq.make_srb([[0], [1, 2], [3]], [2, 4, 16], 30)
# generate XRB circuits using the same arguments as SRB and combine them
circuits += tq.make_xrb([[0], [1, 2], [3]], [2, 4, 16], 30)
# initialize a noisy simulator with stochastic Pauli and overrotation
sim = tq.Simulator().add_stochastic_pauli(px=0.02).add_overrotation(0.04)
# run the circuits on the simulator to populate their results
sim.run(circuits, n_shots=1000)
# print the fit summary
circuits.fit()
[2]:
|
SRB
Streamlined Randomized Benchmarking
|
Cliffords
(0,)
|
Cliffords
(1, 2)
|
Cliffords
(3,)
|
|
${e}_{F}$
The probability of an error acting on the targeted systems during a random gate.
|
2.3e-02 (9.2e-04)
0.022546702265275387, 0.0009215562372938647
|
3.9e-02 (1.4e-03)
0.039390934498134654, 0.0013605019056547535
|
2.3e-02 (1.3e-03)
0.02257337747897606, 0.001311001388838058
|
|
${p}$
Decay parameter of the exponential decay $Ap^m$.
|
9.7e-01 (1.2e-03)
0.9699377303129662, 0.0012287416497251528
|
9.6e-01 (1.5e-03)
0.9579830032019897, 0.0014512020326984038
|
9.7e-01 (1.7e-03)
0.9699021633613653, 0.0017480018517840772
|
|
${A}$
SPAM parameter of the exponential decay $Ap^m$.
|
9.5e-01 (5.7e-03)
0.9513819667382615, 0.00571052829124158
|
9.2e-01 (8.7e-03)
0.9156933658449761, 0.008666118251208018
|
9.5e-01 (8.1e-03)
0.9527285904401025, 0.008105648773833228
|
|
XRB
Extended Randomized Benchmarking
|
Cliffords
(0,)
|
Cliffords
(1, 2)
|
Cliffords
(3,)
|
|
${e}_{U}$
The process infidelity of the coherent error acting on the specifed systems during a random gate.
|
2.8e-03 (1.2e-03)
0.0027961748426389987, 0.0011867621820910682
|
7.4e-04 (1.8e-03)
0.0007413755541452946, 0.0018499766276306052
|
2.5e-03 (1.5e-03)
0.002496651227054364, 0.001516924281228677
|
|
${e}_{S}$
The probability of a stochastic error acting on the specified systems during a random gate.
|
2.0e-02 (7.5e-04)
0.019750527422636388, 0.000747755694292145
|
3.9e-02 (1.3e-03)
0.03864955894398936, 0.0012535741252472032
|
2.0e-02 (7.6e-04)
0.020076726251921695, 0.0007631085332020745
|
|
${u}$
The unitarity of the noise, that is, the average decrease in the purity of an initial state.
|
9.5e-01 (2.0e-03)
0.947852037984266, 0.001954632333190921
|
9.2e-01 (2.6e-03)
0.9191409818864918, 0.00257093128149931
|
9.5e-01 (2.0e-03)
0.9469994965775348, 0.0019941008322145893
|
|
${A}$
SPAM parameter of the exponential decay $Au^m$.
|
9.6e-01 (1.0e-02)
0.9612316434977186, 0.010011585936591313
|
9.8e-01 (1.1e-02)
0.9826515503622386, 0.01089700175280817
|
9.7e-01 (1.1e-02)
0.9650706917040588, 0.010815743551143037
|
Notice that the fit() output contains an estimate
of process infidelity for the specified systems from SRB, the stochastic
infidelity from XRB, and the unitary infidelity which would be absent if the
circuit collection did not contain both SRB and XRB circuits. We
can visualize the different process infidelities as follows.
[3]:
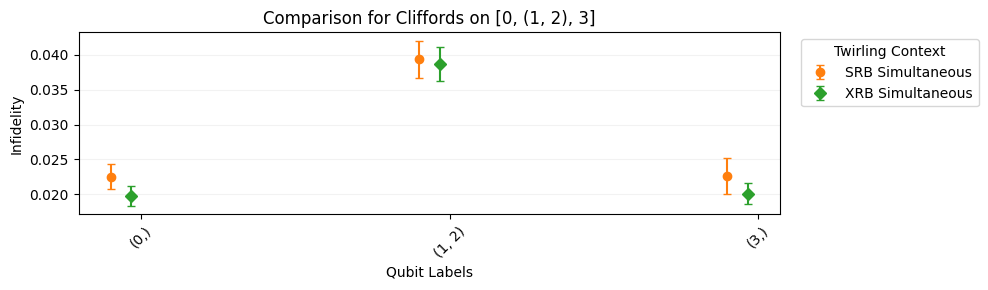
# plot a comparison of process infidelities
circuits.plot.compare_rb()
Download
Download this file as Jupyter notebook: srb_xrb_example.ipynb.
