Math
Decomposes a target multi-qubit |
|
Finds two unitary matrices whose tensor product is closest to the specified matrix. |
|
Enumerates possible qubit gate decomposition modes. |
|
Exhaustively attempts to split all |
|
Accepts a matrix representing an operator acting on |
|
Returns the smallest positive integer \(d\) such that \(x=d^n\) for some positive integer \(n\). |
|
Returns a new unitary where extra dimensions have been added to every subsystem and the given unitary has been embedded into the lowest energy levels. |
|
Returns the integer solution to |
|
Returns the integer logarithm of |
|
Returns the Kronecker product of all supplied arrays (two or more). |
|
Constructs a confusion matrix from a single error probability or a vector of error probabilities. |
|
If the given number is a power of a prime number less than 20, returns the prime. |
|
Calculates the process infidelity between two unitary matrices. |
|
Reshuffles the subsystems of a multi-partite matrix. |
|
Computes the projective order of a unitary matrix, that is, the smallest positive integer such that the matrix to the power of that integer is proportional to the identity. |
|
Finds a gate inside of a |
|
Decomposes an arbitrary two-qubit gate using the KAK decomposition. |
|
Returns a random CPTP superoperator matrix drawn from the BCSZ distribution ([16]). |
|
Returns a random density matrix drawn from the trace-normalized Ginibre ensemble of the given rank. |
|
Returns a Haar-random unitary matrix of size |
|
A fixed unitary rotation. |
|
Parent class for |
|
A representation of a rotation of the form \(exp^{-i \cdot G \cdot \text{param}}\) for some Hermitian matrix \(G\). |
|
Represents a quantum superoperator. |
|
Represents an operator (e.g., unitary) or superoperator (e.g., CPTP channel) on a multipartite qubit system. |
|
Represents a pure or mixed state on a multipartite qubit system. |
|
Represents a multipartite tensor on an arbitrary number of subsystems. |
|
Returns the superoperator of the operation \(X\mapsto AXB^T\) in the subsystem-wise row stacking basis. |
|
Base class for symplectic representations of collections and mappings of qudit Weyl operators. |
|
Represents the decomposition of a multi-qudit operator in the Weyl operator basis. |
|
Represents a list of multi-qudit projective Weyl operators. |
|
Represents a set of multi-qudit projective Weyl operators. |
|
Represents a multi-qudit Clifford operator via its symplectic representation. |
|
Class that represents a list of multi-qudit Weyl operators with associated phases that are constrained to certain discrete values on the unit circle. |
|
A class which stores the symplectic representation of an Abelian group of multi-qudit stabilizer operators. |
Decomposition tools
- trueq.math.decomposition.decompose_unitary(given_gate, target_gate, max_depth=3, tol=1e-10, dim=None, max_resets=20)
Decomposes a target multi-qubit
Gateinto alternating cycles of local operations and the given multi-qubitGate.import trueq as tq circuit = tq.math.decompose_unitary(tq.Gate.cx, tq.Gate.swap) circuit.draw()
- Parameters:
max_depth (
int) – The maximum number ofgiven_gates to use in the decompostion.tol (
float) – The tolerance for convergence as defined by process infidelity.dim (
int|NoneType) – The dimension of the subsystems. The default value ofNonewill result in the dimension inferred fromgiven_gate.max_resets (
int) – The number of times to attempt to reset the algorithm.
- Returns:
A circuit that implements the target gate up to a global phase.
- Return type:
- trueq.math.decomposition.dekron(A, dim=None, force=False)
Finds two unitary matrices whose tensor product is closest to the specified matrix.
import numpy as np import trueq as tq U = np.diag([1, 1, -1, -1]) print(tq.math.dekron(U, dim=2, force=True))
(array([[ 1.+0.j, 0.+0.j], [ 0.+0.j, -1.+0.j]]), array([[1.+0.j, 0.+0.j], [0.+0.j, 1.+0.j]]))- Parameters:
A (
numpy.array) – A matrix to decompose into a tensor product of two unitary matrices.dim (
int|NoneType) – Dimension of the first square submatrixa. The default value ofNonewill result in the dimension inferred froma.force (
bool) – Whether to force a decomposition to the nearest tensor factors (True) or raise an error if no exact decomposition is found (False).
- Returns:
The closest unitary tensor factors of the input matrix.
- Return type:
tuple- Raises:
DecompError – if
force=Falseand no valid decomposition is found.
- class trueq.math.decomposition.QubitMode(value)
Enumerates possible qubit gate decomposition modes. A decomposition mode of ZXZ, for example, results in decompositions of the form
[("Z", angle1), ("X", angle2), ("Z", angle3)], where entries appear in chronological order, and angles are specified in degreesSome decomposition modes contain 5 rotation axes, such as ZXZXZ. These modes rely on identities of the form \(R_X(\theta)=R_Z(-\pi/2)R_X(\pi/2)R_Z(\pi-\theta)R_X(\pi/2)R_Z(-\pi/2)\). Therefore, these modes guarantee that the second and fourth rotation are always +90 degrees. This is useful when virtual gates are used for one rotation axis. If virtual Z gates are used, and the mode is ZXZXZ, then gates will be decomposed in the form
[("Z", angle1), ("X", 90), ("Z", angle2), ("X", 90), ("Z", angle3)]and only one pulse shape is required to create any single qubit unitary.- decompose(gate)
Decomposes the given gate into this mode, where the output format is a list of tuples of the form
(pauli, angle).import trueq as tq tq.math.QubitMode.ZXZ.decompose(tq.Gate.y)
[('Z', 0.0), ('X', 180.0), ('Z', 180.0)]- Returns:
A list of axes and angles to generate the gate from this mode.
- Return type:
list
- trueq.math.decomposition.split_cycle(cycle, max_size=6)
Exhaustively attempts to split all
Gates in thisCycleintoGates that act on as few subsystems as possible.import trueq as tq # Generate a three-qubit gate from a product of seperate single-qubit gates. # This is done using the & shorthand for Kronecker product. gate = tq.Gate.s & tq.Gate.h & tq.Gate.y cycle = tq.Cycle({(0, 1, 2): gate}) tq.math.split_cycle(cycle)
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".- Marker 0
Compilation tools may only recompile cycles with equal markers.(0): Gate.s- Name:
-
- Gate.s
- Aliases:
-
- Gate.s
- Gate.sz
- Gate.cliff9
- Generators:
-
- 'Z': 90.0
- Matrix:
-
-
1.00j -1.00
-
(1): Gate.h- Name:
-
- Gate.h
- Aliases:
-
- Gate.h
- Gate.f
- Gate.cliff12
- Generators:
-
- 'X': 127.279
- 'Z': 127.279
- Matrix:
-
-
0.71 0.71 0.71 -0.71
-
(2): Gate.y- Name:
-
- Gate.y
- Aliases:
-
- Gate.y
- Gate.cliff2
- Generators:
-
- 'Y': 180.0
- Matrix:
-
-
-1.00 1.00
-
Note
The cost of this function scales exponentially with the number of qubits. Setting
max_sizeto be greater than6for qubits could result in extremely long delays.
General tools
- trueq.math.general.add_subsystems(mat, labels, all_labels)
Accepts a matrix representing an operator acting on
labels, which is then reshuffled based on the ordering ofall_labels. For each subsystem inall_labelsnot contained inlabels, an identity matrix is inserted in the returned matrix, respecting the order ofall_labels.For example, given the matrix representation of \(X \otimes Z \otimes Y\),
labelsof(0, 2, 3), and a targetall_labelsof(2, 1, 0, 3), this method would return the matrix reperesentation of \(Z \otimes I \otimes X \otimes Y\).- Parameters:
mat (
ndarray) – The matrix which is being manipulated.labels (
tuple) – The current labels associated with the provided matrix.all_labels (
tuple) – The target label ordering, including any new labels.
- Return type:
ndarray- Raises:
ValueError – If
labelsis not a strict subset ofall_labels, or if there are repeat labels in either tuple, or ifmathas an incompatible shape withlabels.
- trueq.math.general.auto_base(x)
Returns the smallest positive integer \(d\) such that \(x=d^n\) for some positive integer \(n\). This is always possible due to the trivial choice \(d=x\) and \(n=1\). This function can be used to figure out a suitable subsystem dimension when only the total dimension of a composite system is known. See also
int_base()andprime_base().import trueq as tq assert tq.math.auto_base(512) == 2 assert tq.math.auto_base(36) == 6 assert tq.math.auto_base(21) == 21
- Parameters:
x (
int) – A positive integer.- Return type:
int
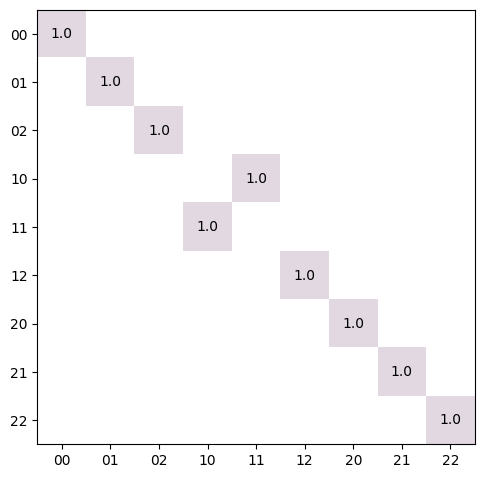
- trueq.math.general.embed_unitary(u, n_sys, extra_dims)
Returns a new unitary where extra dimensions have been added to every subsystem and the given unitary has been embedded into the lowest energy levels. The returned unitary acts trivially on the extra levels.
import trueq as tq # inject the CNOT gate into two qutrits cnot3 = tq.math.embed_unitary(tq.Gate.cnot.mat, 2, 1) tq.plot_mat(cnot3, xlabels=3, ylabels=3)
- Parameters:
u (
numpy.ndarray-like) – The unitary matrix to embed.n_sys (
int) – The number of subsystems the unitary acts on.extra_dims – The number of extra dimensions to add to each subsystem.
- Returns:
An embedding of
uinto a larger space.- Return type:
int
- trueq.math.general.int_base(x, n)
Returns the integer solution to
base ** n == x. ReturnsNonewhen no exact solution exists to numerical precision. See alsoprime_base(),auto_base(), andint_log().import trueq as tq print(tq.math.int_base(16, 4)) print(tq.math.int_base(9, 2)) print(tq.math.int_base(12, 2))
2 3 None
- Parameters:
x (
int) – The positive integer to find the base of.n – A positive integer; the power to which the base should be raised to get
x.
- Returns:
The integer solution to
base ** n == x.- Return type:
int|NoneType
- trueq.math.general.int_log(x, base)
Returns the integer logarithm of
xin the givenbase. ReturnsNonewhen no exact solution exists to numerical precision. See alsoint_base().import trueq as tq print(tq.math.int_log(16, 2)) print(tq.math.int_log(16, 4)) print(tq.math.int_log(16, 3))
4 2 None
- Parameters:
x (
int) – The positive integer to compute the logarithm of.base (
int) – The base of the logarithm.
- Returns:
The integer logarithm in a specified base.
- Return type:
int|NoneType
- trueq.math.general.kron(*arrs)
Returns the Kronecker product of all supplied arrays (two or more). Note that this function does not work with numpy.complex128 data type.
- Parameters:
*arrs – One or more numpy.ndarrays.
- Returns:
The Kronecker product of the specified arrays.
- Return type:
numpy.ndarray
- trueq.math.general.make_confusion_matrix(error, n_sys=1, dim=None, n_outcomes=None)
Constructs a confusion matrix from a single error probability or a vector of error probabilities. If a matrix is given, it is checked to have columns that sum to unity before being returned.
If \(p\) is the single probability error or a vector of error probabilities, it is turned into confusion matrix by setting the diagonal elements to \(1-p\) and the off-diagonal elements of the first
m = \text{min}(n_o, d)^ncolumns to \(p/(n_o - 1)\), and the elements of the remaining columns to \(p/n_o\), where \(n\) isn_sys, \(d\) isdim, and \(n_o\) isn_outcomes. Typically, one will want \(d=n_o\), which is the default behaviour.import trueq.math as tqm print(tqm.make_confusion_matrix(0.01)) print(tqm.make_confusion_matrix([0.1, 0.2, 0.3]))
[[0.99 0.01] [0.01 0.99]] [[0.9 0.1 0.15] [0.05 0.8 0.15] [0.05 0.1 0.7 ]]
- Parameters:
error (
float|array_like) – An error probability, a vector of error probabilities, or a matrix whose columns sum to unity.n_sys (
int) – The number of subsystems.dim (
int) – The dimension of each subsystem.dim – The number of outcomes.
- Return type:
numpy.ndarray- Raises:
ValueError – If the columns of the output do not sum to unity or if any entry is negative.
ValueError – If any provided dimensions are not consistent with the value of
error.
- trueq.math.general.prime_base(n)
If the given number is a power of a prime number less than 20, returns the prime. Otherwise, returns
None. See alsoint_base()andauto_base().- Parameters:
n (
int) – The number to check.- Return type:
int|NoneType
- trueq.math.general.proc_infidelity(A, B=None)
Calculates the process infidelity between two unitary matrices.
- Parameters:
A (
numpy.ndarray) – A unitary matrix of shape(d, d).B (
numpy.ndarray|NoneType) – A unitary matrix of shape(d, d). IfBisNone, then its assumed to be an identity and a faster calculation takes place.
- Returns:
The process infidelity between the two unitary matrices.
- Return type:
float
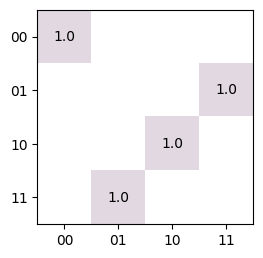
- trueq.math.general.reshuffle(mat, perm)
Reshuffles the subsystems of a multi-partite matrix.
import numpy as np import trueq as tq # Cnot on qubits (0, 1) mat = np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 0, 1], [0, 0, 1, 0]]) # We can reverse the direction of the CNOT matrix so that the control qubit # becomes 1 instead of 0: tq.plot_mat(tq.math.reshuffle(mat, [1, 0]), xlabels=2, ylabels=2)
- Parameters:
mat (
numpy.ndarray) – Anumpy.ndarrayobject to be reshuffled, which must have an(n, n)shape wheren = dim ** len(perm).perm (
Iterable) – A list of indices to permute which must contain all integers from 0 to the number of systems in the mat.
- Returns:
The reshuffled matrix.
- Return type:
numpy.ndarray
- trueq.math.general.unitary_order(mat, max_order=10)
Computes the projective order of a unitary matrix, that is, the smallest positive integer such that the matrix to the power of that integer is proportional to the identity.
import trueq as tq # the cnot is of order two print(tq.math.unitary_order(tq.Gate.cx)) # the projective order is independent of a global phase, so we can multiply # by a phase and get the same order print(tq.math.unitary_order(1j * tq.Gate.cx.mat))
2 2
- Parameters:
mat (
ndarray) – The matrix to compute the projective order of.max_order (
int) – The maximum order to allow.
- Return type:
int- Raises:
ValueError – If
matis not a unitary matrix, or if the projective order ofmatexceedsmax_order.
KAK tools
- trueq.math.kak_utils.kak(u)
Decomposes an arbitrary two-qubit gate using the KAK decomposition.
As seen in the example below, the decomposition is of the form \(u=(a_0 \otimes a_1) K (b_0 \otimes b_1)\) where \(K=\exp(-i(k_0 XX+k_1 YY+k_2 ZZ)\pi/360)\). Note that the unitary equality does not guarantee the global phase. The vector of angles \(k\) is chosen uniquely to satisfy \(90 \ge k_0 \ge k_1 \ge |k_2|\) and \(k_2 \ge 0\) whenever \(k_0=90\).
import trueq as tq a, b, k = tq.math.kak(tq.Gate.cnot) gen = {p: v for p, v in zip(["XX", "YY", "ZZ"], k)} tq.Gate(np.kron(*a) @ tq.Gate.from_generators(gen).mat @ np.kron(*b))
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".- Name:
-
- Gate.cx
- Aliases:
-
- Gate.cx
- Gate.cnot
- Likeness:
-
- CNOT
- Generators:
-
- 'ZX': -90.0
- 'IX': 90.0
- 'ZI': 90.0
- Matrix:
-
-
0.71 -0.71j 0.71 -0.71j 0.71 -0.71j 0.71 -0.71j
-
- Parameters:
u (
Gate) – A two-qubit gate.- Returns:
A decomposition of the input.
- Return type:
tuple
- trueq.math.kak_utils.find_kak_equivalent(conf, gate, param_scaling=180, tol=0.01)
Finds a gate inside of a
Configthat is equivalent to the target gate up to single-qubit operations.- Parameters:
conf (
Config) – AConfigobject containing multi-qubit gates.gate (
Gate) – The target gate to find inside the config.param_scaling (
float) – Upper bound on the parameter range that is searched to match parameter values for parametrized gates.tol (
float) – Tolerance to decide if convergence was successful, success is defined as the L1 distance between target KAK and found KAK is less than the tol.
- Returns:
a list of
Gates that are equivalent to the target.- Return type:
list
Random Generators
- trueq.math.random.random_bcsz(dim, rank=None)
Returns a random CPTP superoperator matrix drawn from the BCSZ distribution ([16]). The superoperator is in the global row stacking basis.
See also
random_bcsz()which invokes this method to create a newSuperop()object.- Parameters:
dim (
int) – The dimension the superoperator will act on.rank (
int|NoneTye) – A positive integer specifying the output Choi rank. IfNone, then the valuedim ** 2is used. A value of1results in a random unitary superoperator.
- Returns:
A matrix of shape
(dim**2, dim**2).- Return type:
numpy.ndarray
- trueq.math.random.random_density(dim, rank=1)
Returns a random density matrix drawn from the trace-normalized Ginibre ensemble of the given rank. By default, the rank is one so that this function returns random pure states.
- Parameters:
dim (
int) – The dimension of the density matrix.rank (
int) – A positive integer specifying the rank of the output density matrix.
- Returns:
A random density matrix of a specified matrix rank.
- Return type:
numpy.ndarray
- trueq.math.random.random_unitary(dim)
Returns a Haar-random unitary matrix of size
(dim, dim).See also
random_unitary()which invokes this method to create a newSuperop()object.- Parameters:
dim (
int) – The size of the unitary matrix.- Returns:
A Haar-random unitary matrix.
- Return type:
numpy.ndarray
Rotations
- class trueq.math.rotation.FixedRotation(mat)
A fixed unitary rotation.
import trueq as tq import numpy as np from trueq.math import FixedRotation g = FixedRotation(tq.Gate.x.mat) assert g.pauli_angle == ("X", 180)
- Parameters:
mat (
numpy.array) – A Unitary matrix.
- property pauli_angle
If this layer can be represented by a fixed rotation along a Pauli axis such as \(exp^{-i \cdot \frac{\pi}{360} \text{Pauli} \cdot \text{angle}}\), this will be a tuple
(Pauli, angle), otherwise this is(None, None)import trueq as tq from trueq.math import FixedRotation g = FixedRotation.from_pauli("XY", 90) assert g.pauli_angle == ("XY", 90) g = FixedRotation.from_pauli("Y", 11) assert g.pauli_angle == ("Y", 11)
- Type:
tuple
- static from_pauli(pauli, angle)
A convenience method to create a
FixedRotationfrom a Pauli string.This is the equivalent to \(exp^{-i \frac{\pi}{360} \text{pauli} \cdot \text{angle}}\).
import trueq as tq from trueq.math import FixedRotation gen = FixedRotation.from_pauli("XY", 90) assert gen.pauli_angle == ("XY", 90) gen = FixedRotation.from_pauli("Y", 11) assert gen.pauli_angle == ("Y", 11)
- Parameters:
pauli (
str) – A Pauli which describes the axis of the rotation.angle (
float) – The angle of rotation as defined above.
- Return type:
- property width
The width of the matrix returned by this layer.
- Type:
int
- class trueq.math.rotation.Layer
Parent class for
RotationandFixedRotation.- property pauli_angle
If this layer can be represented by a fixed rotation along a Pauli axis such as \(exp^{-i \cdot \frac{\pi}{360} \text{Pauli} \cdot \text{angle}}\), this will be a tuple
(Pauli, angle), otherwise this is(None, None)import trueq as tq from trueq.math import FixedRotation g = FixedRotation.from_pauli("XY", 90) assert g.pauli_angle == ("XY", 90) g = FixedRotation.from_pauli("Y", 11) assert g.pauli_angle == ("Y", 11)
- Type:
tuple
- property pauli_const
If this layer can be represented by a rotation along a Pauli axis such as: \(exp^{-i \frac{\pi}{360} \text{Pauli} \cdot \text{constant} \cdot \text{param}}\), this will be a tuple
(Pauli, constant), otherwise this is(None, None).import trueq as tq import numpy as np from trueq.math import Rotation g = Rotation(tq.Gate.y.mat * np.pi / 360, "theta") assert g.pauli_const == ("Y", 1) g = Rotation.from_pauli("X", "phi", 5) assert g.pauli_const == ("X", 5) gen = tq.Gate.random(2).mat g = Rotation(gen + gen.conj().T, "theta") assert g.pauli_const == (None, None)
- Type:
tuple
- abstract property width
The width of the matrix returned by this layer.
- Type:
int
- class trueq.math.rotation.Rotation(gen, param_name)
A representation of a rotation of the form \(exp^{-i \cdot G \cdot \text{param}}\) for some Hermitian matrix \(G\).
import trueq as tq import numpy as np from trueq.math import Rotation g = Rotation(tq.Gate.x.mat / 2, "theta") assert tq.Gate(g(np.pi / 2)) == tq.Gate.cliff5 pauli, const = g.pauli_const assert pauli == "X" assert abs(const - 180 / np.pi) < 1e-12
- Parameters:
gen (
numpy.array) – A Hermitian matrix to generate this rotation.param_name (
str) – The name associated with theparam, e.g.theta,phi,t, etc.
- property pauli_const
If this layer can be represented by a rotation along a Pauli axis such as: \(exp^{-i \frac{\pi}{360} \text{Pauli} \cdot \text{constant} \cdot \text{param}}\), this will be a tuple
(Pauli, constant), otherwise this is(None, None).import trueq as tq import numpy as np from trueq.math import Rotation g = Rotation(tq.Gate.y.mat * np.pi / 360, "theta") assert g.pauli_const == ("Y", 1) g = Rotation.from_pauli("X", "phi", 5) assert g.pauli_const == ("X", 5) gen = tq.Gate.random(2).mat g = Rotation(gen + gen.conj().T, "theta") assert g.pauli_const == (None, None)
- Type:
tuple
- static from_pauli(weyl, param_name, constant=1, dim=None)
A convenience method to create a
Rotationfrom a Pauli or Weyl string.This is the equivalent to \(exp^{-i \frac{\pi}{360} W_h \cdot \text{constant} \cdot \text{param}}\), where \(W_h\) is the Hermitian version of weyl defined via
herm_mat.import trueq as tq from trueq.math import Rotation gen = Rotation.from_pauli("XY", "theta") assert gen.pauli_const[0] == "XY" gen = Rotation.from_pauli("XY", "theta", constant=10) assert gen.pauli_const == ("XY", 10) gen = Rotation.from_pauli("W01", "theta", dim=3) gen(90)
array([[1. +0.j , 0. +0.j , 0. +0.j ], [0. +0.j , 0.57195234+0.82028685j, 0. +0.j ], [0. +0.j , 0. +0.j , 0.57195234-0.82028685j]])Note
The methods
from_pauli()andfrom_weyl()are identical. They both exist to make searching the documentation easier.- Parameters:
weyl (
str) – A Weyl string which describes the axis of the rotation.param_name (
str) – The name of the associated free parameter.constant (
float) – A constant scaling term as defined above.dim – The qudit dimension, which must be one of
SMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().
- Return type:
- static from_weyl(weyl, param_name, constant=1, dim=None)
A convenience method to create a
Rotationfrom a Pauli or Weyl string.This is the equivalent to \(exp^{-i \frac{\pi}{360} W_h \cdot \text{constant} \cdot \text{param}}\), where \(W_h\) is the Hermitian version of weyl defined via
herm_mat.import trueq as tq from trueq.math import Rotation gen = Rotation.from_pauli("XY", "theta") assert gen.pauli_const[0] == "XY" gen = Rotation.from_pauli("XY", "theta", constant=10) assert gen.pauli_const == ("XY", 10) gen = Rotation.from_pauli("W01", "theta", dim=3) gen(90)
array([[1. +0.j , 0. +0.j , 0. +0.j ], [0. +0.j , 0.57195234+0.82028685j, 0. +0.j ], [0. +0.j , 0. +0.j , 0.57195234-0.82028685j]])Note
The methods
from_pauli()andfrom_weyl()are identical. They both exist to make searching the documentation easier.- Parameters:
weyl (
str) – A Weyl string which describes the axis of the rotation.param_name (
str) – The name of the associated free parameter.constant (
float) – A constant scaling term as defined above.dim – The qudit dimension, which must be one of
SMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().
- Return type:
- property width
The width of the matrix returned by this layer.
- Type:
int
- property id_scale
An estimate of a non-zero value where this rotation is identity.
If the rotation is “well behaved”, such as a rotation around a Pauli axis, this value will typically be the smallest non-zero value where the rotation is the identity.
If no reasonable estimate can be calculated, then this value is
None.import trueq as tq import numpy as np gen = np.flipud(np.eye(5)) rot = tq.math.Rotation(gen, "phi") assert rot.id_scale is not None assert tq.math.proc_infidelity(rot(rot.id_scale)) < 1e-12 # D matrix where the terms are irrational fractions of one another rot2 = tq.math.Rotation(np.diag([0, 1, np.sqrt(2), np.pi]), "phi") assert rot2.id_scale is None
- Type:
float|NoneType
- find_closest(mat, tol=1e-12)
Attempts to find the parameter value where this rotation creates a matrix which is equal to the target matrix up to a global phase.
If no suitable parameter value is found, then this returns
Noneimport trueq as tq import numpy as np gen = np.flipud(np.eye(5)) rot = tq.math.Rotation(gen, "phi") target = rot(0.5) assert rot.find_closest(target) == 0.5 assert rot.find_closest(tq.math.random_density(5)) is None
- Parameters:
mat (
numpy.array) – The target matrix.tol (
float) – Allowable process infidelity to be considered a match.
- Return type:
NoneType|float
Superoperators
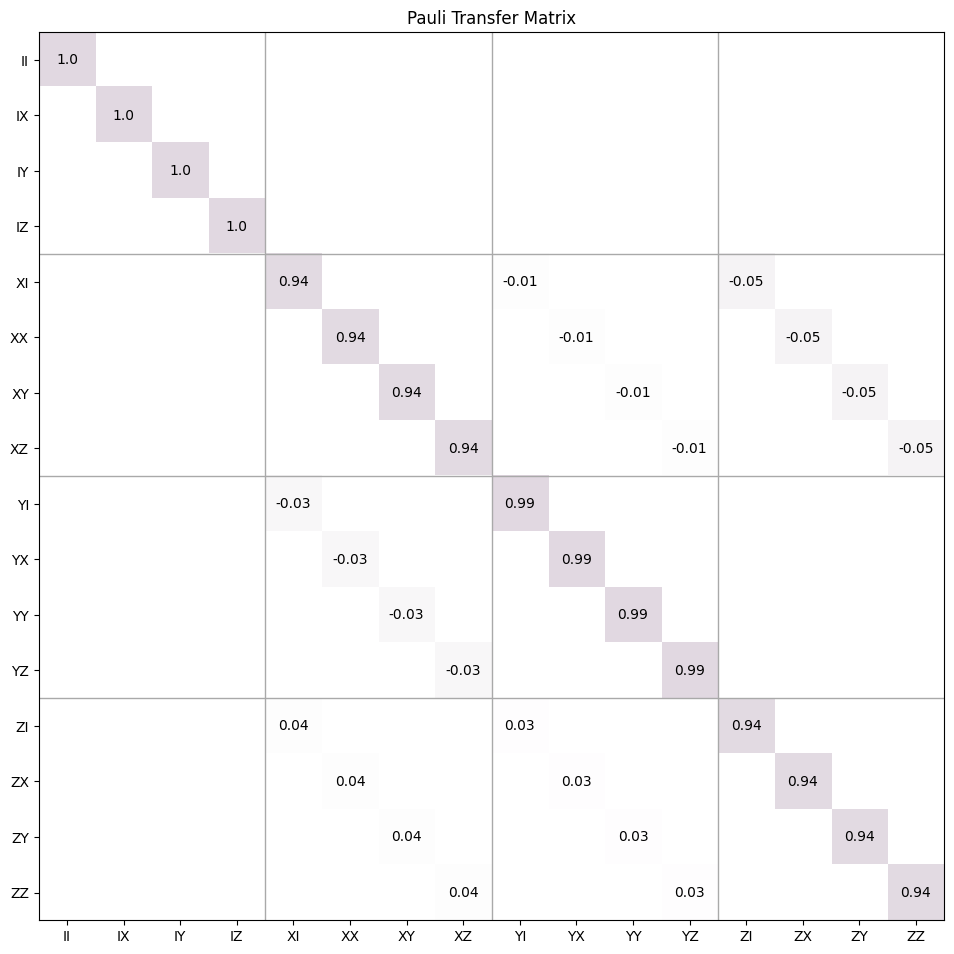
- class trueq.math.superop.Superop(mat, dim=None)
Represents a quantum superoperator. A superoperator is a linear operation that maps density matrices to density matrices. This class contains utilities to compute various superoperator properties and metrics, methods for composing and combining superoperators, and methods to convert between the various superoperator representations.
Generally, instances of this class should be created by calling one of the static methods starting with
from_. For example:import numpy as np import trueq as tq k1 = np.sqrt(0.95) * np.eye(2) k2 = np.sqrt(0.05) * tq.math.random_unitary(2) s = tq.math.Superop.from_kraus([k1, k2]) # whether s is cp and tp, and print the choi rank print(s.is_cp, s.is_tp, s.choi_rank) # compute some metrics of u print(s.infidelity, s.coherent_infidelity) # apply s to a random density matrix print(s.apply(tq.math.random_density(2))) # compute the 2-norm distance to the identity channel i = tq.math.Superop.from_unitary(np.eye(2)) print((s - i).norm(2)) # plot the pauli transfer matrix of s tensored with i (s & i).plot_ptm()
True True 2 0.033112796355804 0.0011446589119764594 [[0.71205042-5.83827342e-20j 0.36363279-2.06758918e-01j] [0.36363279+2.06758918e-01j 0.28794958+8.32318907e-19j]] 0.11508743868173268
- Parameters:
mat (
numpy.ndarray-like) – A superoperator matrix in the row-stacking basis.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- property dim
The dimension of each subsystem. For example, this is equal to
2for a superoperator that acts on two qubits.- Type:
int
- property n_sys
The number of subsystems that this superoperator acts on.
- Type:
int
- property total_dim
The total Hilbert space dimension that this superoperator acts on.
- Type:
int
- property choi_rank
The rank of the Choi matrix of this superoperator, that is, the minimal number of Kraus operators required to describe this superoperator.
- Type:
int
- property is_cp
Whether this superoperator is completely positive (CP), i.e. whether this superoperator always outputs positive states when given positive states (even when this superoperator is tensored with an ancilla space).
- Type:
bool
- property is_cptp
Whether this superoperator is completely positive and trace-preserving (CPTP). See also
is_cpandis_tp.- Type:
bool
- property is_tp
Whether this superoperator is trace preserving (TP), i.e. whether the trace of output density matrices is always equal to the trace of input density matrices.
- Type:
bool
- property is_unital
Whether this superoperator is unital, i.e. whether it maps the completely mixed state to the completely mixed state.
- Type:
bool
- property is_unitary
Whether this superoperator is a unitary chanel, i.e. whether there existis a unitary \(U\) such this superoperator acts as \(U\rho U^\dagger\) for any input \(\rho\). If so, it can be extracted as the sole Kraus operate using
kraus.- Type:
bool
- property avg_gate_fidelity
The average gate fidelity of this superoperator, defined by
\[\overline{F} = \int d\psi \langle\psi|\mathcal{E}(|\psi\rangle\langle\psi|)|\psi\rangle\]for the superoperator \(\mathcal{E}\). This is related to the process fidelity \(F_E\) (see
fidelity) via \(\overline{F}=(d^2F_E+d)/(d(d+1))\) where \(d\) is the dimension of the underlying Hilbert space.import trueq.math as tqm s = tqm.Superop(tqm.random_bcsz(3)) u = tqm.Superop.from_unitary(tqm.random_unitary(3)) # find the average gate fidelity between these superoperators (s @ u.adj).avg_gate_fidelity
0.3492135741087097
- Type:
float
- property avg_gate_infidelity
The average gate infidelity of this superoperator, often denoted as \(r\), equal to one minus
avg_gate_fidelity; see the definition there.import trueq.math as tqm s = tqm.Superop(tqm.random_bcsz(3)) u = tqm.Superop.from_unitary(tqm.random_unitary(3)) # find the average gate infidelity between these superoperators (s @ u.adj).avg_gate_infidelity
0.7025523156937101
- Type:
float
- property coherent_infidelity
The coherent infidelity of this superoperator, defined by
\[e_U = e_F - e_S\]for the superoperator \(\mathcal{E}\), where \(e_F\) is the process
infidelityand \(e_S\) is thestochastic_infidelity. This quantity ranges between 0 and the processinfidelityof this superoperator, where a larger value indicates more coherent (i.e. unitary or calibration) noise. This quantity is reported by the XRB protocol when SRB results are also present to estimate \(e_F\).- Type:
float
- property dnorm
The diamond norm of this superoperator.
import trueq as tq # ideal gate s1 = tq.math.Superop.from_unitary(tq.Gate.cnot.mat) # gate simulated with depolarizing sim = tq.Simulator().add_depolarizing(0.01) s2 = sim.operator(tq.Cycle({(0, 1): tq.Gate.cnot})).mat() s2 = tq.math.Superop.from_rowstack(s2) # compute the diamond norm of the difference (see the note below for why # this is commented out) # (s1 - s2).dnorm
Note
This is computed via Watrous’ semidefinite program, see [17].
Note
This function requires
cvxpyandcvxoptto be properly installed. In particular, their dependencyscsmust also be installed, which also requiresblasandlapacklibraries to be installed. It may take some effort to get this all set up in your environment, hence the example above hasdnormcommented out so that the documentation will build.- Type:
float
- property fidelity
The process fidelity of this superoperator, which can be defined as
\[F_E = \operatorname{Tr}(\mathcal{E})/d^2\]for the superoperator \(\mathcal{E}\) where \(d\) is the dimension of the underlying Hilbert space. This quantity is related to the average gate fidelity \(\overline{F}\) (see
avg_gate_fidelity) via \(\overline{F}=(d^2F_E+d)/(d(d+1))\).import trueq.math as tqm s = tqm.Superop(tqm.random_bcsz(3)) u = tqm.Superop.from_unitary(tqm.random_unitary(3)) # find the process fidelity between these superoperators (s @ u.adj).fidelity
0.11035610260696724
- Type:
float
- property infidelity
The process infidelity of this superoperator, defined as \(e_F=1-F_E\) where \(F_E\) is the process
fidelity. This quantity is estimated by protocols like SRB and CB.import trueq.math as tqm s = tqm.Superop(tqm.random_bcsz(3)) u = tqm.Superop.from_unitary(tqm.random_unitary(3)) # find the process infidelity between these superoperators (s @ u.adj).infidelity
0.8747691876486522
- Type:
float
- norm(p=2)
Returns the Schatten p-norm of this superoperator, equal to
\[\|\mathcal{E}\|_p = ( \operatorname{Tr}[(\mathcal{E}^\dagger\mathcal{E})^{p/2}])^{1/p} )\]for the superoperator \(\mathcal{E}\). These norms are unitarily invariant, so the basis (row-stacking, column-stacking, normalized Weyl, etc.) is irrelevant. Certain values of \(p\) have special names:
\(p=1\) is the trace norm.
\(p=2\) is the Frobenius norm and is the fastest to compute.
\(p=\infty\) is the spectral (or operator) norm.
- Parameters:
p (
float) – Any real number greater than or equal to one.- Return type:
float- Raises:
ValueError – If \(p<1\).
- property stochastic_infidelity
The stochastic infidelity of this superoperator, defined by
\[e_S = 1 - \sqrt{\operatorname{Tr}(\mathcal{E}\mathcal{E}^\dagger)} / d\]for the superoperator \(\mathcal{E}\), where \(d\) is the dimension of Hilbert space, see [8]. This quantity ranges between 0 and the process
infidelityof this superoperator, where a larger value indicates more stochastic noise. The stochastic infidelity is reported by the XRB protocol. For unital TP maps, the stochastic fidelity is related to theunitarityby the formula\[e_S = 1 -\sqrt{u(1-1/d^2)+1/d^2}\]- Type:
float
- property unitary_fraction
The unitary fraction of this superoperator, defined as
\[f_u = 1 - (1-1/d^2)\frac{1 - \sqrt{u}}{e_F}\]where \(e_F\) is the process
infidelityand \(d\) is the dimension of Hilbert space. A unitary fraction equal to 0 represents the least possible amount of unitarity a superoperator can have, given itsfidelity, and a value of 1 represents a unitary superoperator.- Type:
float
- property unitarity
The unitarity of this superoperator, defined by
\[u = \frac{d}{d-1}\int d\psi \operatorname{Tr}[ \mathcal{E}'(|\psi\rangle\langle\psi|) ]\]for the superoperator \(\mathcal{E}\), where
\[\mathcal{E}'(A) = \mathcal{E}(A) - \operatorname{Tr}[\mathcal{E}(A)]\frac{I}{\sqrt{d}}\]is the traceless projection of \(\mathcal{E}\), and where \(d\) is the dimension of the underlying Hilbert space [7]. In other words, the unitarity is the purity of output states averaged over all pure input states, normalized by possible trace-decreasing behaviour. This quantity is estimated by the XRB protocol.
- Type:
float
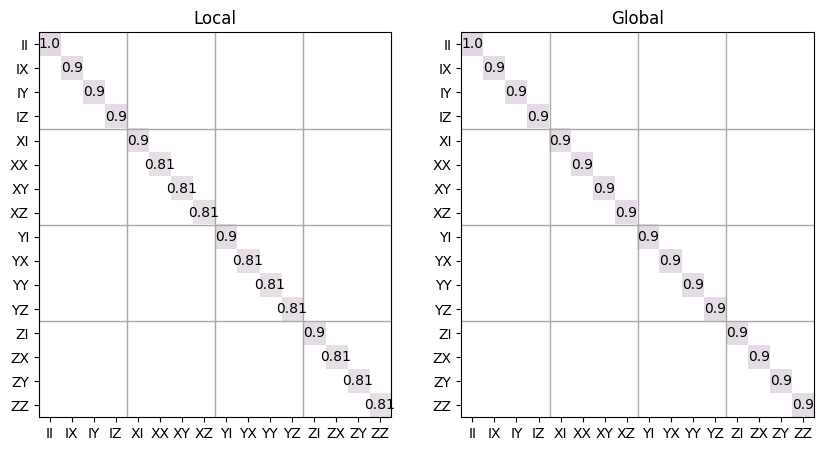
- static depolarizing(p, dim=None, n_sys=1, local=True)
Returns a depolarizing superoperator acting on
n_syssubsystems of dimensiondimof strengthp. For a particular dimensionD, the depolarizing channel is defined as\[\Lambda_D(\rho) = (1-p) \rho + p \text{Tr}(\rho) \mathcal{I} / D\]If
local=True, this function returns the tensor product of single subsystem depolarizing channels, \(\Lambda_d^{\otimes n}\). Otherwise, the global depolarizing channel \(\Lambda_{d^n}\) is returned.import trueq.math as tqm import matplotlib.pyplot as plt # make a local and a global depolarizing channel on two qubits local_dep = tqm.Superop.depolarizing(0.1, n_sys=2) global_dep = tqm.Superop.depolarizing(0.1, n_sys=2, local=False) # plot them as Pauli transfer matrices plt.figure(figsize=(10, 5)) local_dep.plot_ptm(ax=plt.subplot(1, 2, 1)) plt.title("Local") global_dep.plot_ptm(ax=plt.subplot(1, 2, 2)) plt.title("Global")
Text(0.5, 1.0, 'Global')
- Parameters:
dim (
int|NoneType) – The subsystem dimension. The default value ofNonewill result in the default dimension obtained fromget_dim().n_sys (
int) – The number of subsystems.local (
bool) – Whether to return the tensor product of local depolarizing channels or the global depolarizing channel.
- Return type:
- static eye(total_dim, dim=None)
Constructs a new identity superoperator.
- Parameters:
total_dim (
int) – The total dimension the superoperator acts on, e.g.16for four qubits.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Return type:
- static random_bcsz(total_dim, rank=None, dim=None)
Constructs a new random superoperator drawn from the BCSZ distribution ([16]).
import trueq.math as tqm s = tqm.Superop.random_bcsz(9, 5) assert s.is_cptp assert s.choi_rank == 5
- Parameters:
total_dim (
int) – The total dimension the superoperator acts on, e.g.16for four qubits.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().rank (
int|NoneTye) – A positive integer specifying the output Choi rank. IfNone, then the valuetotal_dim ** 2is used. A value of1results in a random unitary superoperator.
- Return type:
- static random_constrained_cptp(total_dim, infidelity, coherent_fraction, equibility=1, rank=None, dim=None)
Constructs a random CPTP (see
is_cptp) channel whose process infidelity and level of unitary are (approximately) given. This is done by composing a random unitary channel of fidelitycoherent_fraction(seerandom_constrained_unitary()) with a random decoherent channel (seerandom_decoherent()) of infidelity(1 - coherent_fraction) * infidelity. The infidelity and stochastic infidelity of the resulting composition is accurate up to \(O(r^2)\) with \(r\) the infidelity, see [8].import trueq.math as tqm # random 2-qutrit gate s = tqm.Superop.random_constrained_cptp(9, 0.01, 0.4) assert s.is_cptp print(s.infidelity, s.stochastic_infidelity)
0.009973805516428236 0.005994386139207886
- Parameters:
total_dim (
int) – The total dimension the superoperator acts on, e.g.16for four qubits.infidelity (
float) – The desired process infidelity; a number in \([0,1]\).coherent_fraction (
float) – The desired fraction of the process infidelity to be unitary or coherent in nature; a number in \([0,1]\).equibility – A positive number indicating the equibility of the resulting channel in arbitrary units. A large value (say,
100) results in very uniform singular values of the leading kraus term, whereas they are more varied for a small value like 1.rank (
int|NoneTye) – A positive integer specifying the output Choi rank. IfNone, then the valuetotal_dim ** 2is used. A value of1results in a random unitary superoperator.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Return type:
- static random_constrained_unitary(total_dim, infidelity, dim=None)
Constructs a random unitary channel constrained to have the given process infidelity, see
infidelity.import trueq.math as tqm s = tqm.Superop.random_constrained_unitary(9, 0.1) assert s.is_unitary assert abs(s.infidelity - 0.1) < 1e-10
- Parameters:
total_dim (
int) – The total dimension the superoperator acts on, e.g.16for four qubits.infidelity (
float) – The desired process infidelity; a number in \([0,1]\).dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Return type:
- static random_decoherent(total_dim, infidelity, equibility=1, rank=None, dim=None)
Constructs a random decoherent channel with a given process infidelity (approximately), see
infidelity. A decoherent channel is one whose polar decomposition of the leading Kraus term (seelkpd()) returns a unitary portion equal to the identity, i.e. the main unitary action of the channel is trivial. The infidelity of the resulting composition is accurate up to \(O(r^2)\) with \(r\) the infidelity, see [8].import trueq.math as tqm s = tqm.Superop.random_decoherent(9, 0.1) assert s.is_cptp print(s.infidelity, s.stochastic_infidelity)
0.09999909357974013 0.09899830938507337
- Parameters:
total_dim (
int) – The total dimension the superoperator acts on, e.g.16for four qubits.infidelity (
float) – The desired process infidelity; a number in \([0,1]\).equibility (
float) – A positive number indicating the equibility of the resulting channel in arbitrary units. A large value (say,100) results in very uniform singular values of the leading kraus term, whereas they are more varied for a small value like1.rank (
int|NoneTye) – A positive integer specifying the output Choi rank. IfNone, then the valuetotal_dim ** 2is used. A value of1results in a random unitary superoperator.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Return type:
- Raises:
ValueError – If the
rankandinfidelityare inconsistent—the rank can only be1when the infidelity is0.0, and vise versa.
- static random_stochastic(total_dim, infidelity, rank=None, dim=None)
Constructs a random stochastic channel with a given process infidelity, see
infidelity. For the purposes of this function, a stochastic channel is one that can be written as convex mixture of orthogonal unitary channels, one of which is the identity, and the rest of which are traceless with evenly distributed eigenvalues. Such a channel is CPTP (seeis_cptp), and the process fidelity is given by the weight of the identity mixture component.The main difference between this method and
random_decoherent()is that this method does not allow non-unital (e.g. \(T_1\) noise is non-unital because the completely mixed state reverts to something with polarization) behaviour or state-dependent leakage.import trueq.math as tqm s = tqm.Superop.random_stochastic(9, 0.1) assert s.is_cptp print(s.infidelity)
0.09999999999999976
- Parameters:
total_dim (
int) – The total dimension the superoperator acts on, e.g.16for four qubits.infidelity (
float) – The desired process infidelity; a number in \([0,1]\).rank (
int|NoneTye) – A positive integer specifying the output Choi rank. IfNone, then the valuetotal_dim ** 2is used. A value of1results in a random unitary superoperator.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Return type:
- Raises:
ValueError – If the
rankandinfidelityare inconsistent—the rank can only be1when the infidelity is0.0, and vise versa.
- static random_unitary(total_dim, dim=None)
Constructs a Haar-random unitary channel.
import trueq.math as tqm s = tqm.Superop.random_unitary(9) assert s.is_unitary
- Parameters:
total_dim (
int) – The total dimension the superoperator acts on, e.g.16for four qubits.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Return type:
- static zero(total_dim, dim=None)
Constructs a new superoperator that sends all inputs to the zero matrix.
- Parameters:
total_dim (
int) – The total dimension the superoperator acts on, e.g.16for four qubits.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Return type:
- static from_chi(chi)
Instantiates a new
Superopfrom a \(\chi\)-matrix in the Pauli basis (or Weyl basis for subsystem dimension greater than two). The \(\chi\)-matrix is also known as the process matrix. For an ordered orthogonal basis \(B_1,\ldots,B_{d^{2n}}\) of \(d^n\times d^n\) complex matrices, the \(\chi\)-matrix of a quantum channel \(\mathcal{E}\) is a matrix \(\chi\) such that\[\mathcal{E}(\rho) = \sum_{i,j}\chi_{ij}B_i \rho B_j^\dagger\]for any density matrix \(\rho\). The basis used is the same as described in
from_ptm(). In particular, the subsystem dimension must be prime.- Parameters:
chi (
numpy.ndarray) – A square matrix.- Returns:
The superoperator for a given \(\chi\)-matrix representation.
- Return type:
- Raises:
ValueError – If the \(\chi\)-matrix does not have a width that is an even power of a small prime number.
- property chi
The \(\chi\)-matrix representation of this superoperator; see
from_chi()for details on this representation.- Type:
numpy.ndarray
- plot_chi(abs_max=None, ax=None)
Plots the \(\chi\)-matrix representation of this superoperator; see
from_chi()for details on this representation.- Parameters:
abs_max (
NoneType|float) – The value to scale absolute values of the matrix by; the value at which plotted colors become fully opaque. By default, this is the largest absolute magnitude of the input matrix.ax (
matplotlib.Axis|NoneType) – An existing axis to plot on. One is created otherwise.
- static from_kraus(*ops, dim=None)
Instantiates a new
Superopfrom a given set of Kraus operators. A superoperator in the Kraus representation is a set of \(m\) operators \({K_0,\ldots,K_{m-1}}\) that act on a given density matrix by the formula \(\rho\mapsto\sum_{i=0}^{m-1}K_i \rho K^\dagger_i\). A superoperator admits a Kraus representation if and only if it is completely positive (seeis_cp), but it is only trace preserving (seeis_tp) if \(\sum_{k=0}^{m-1}K^\dagger_i K_i = \mathbb{I}\).import numpy as np import trueq as tq # instantiate a depolarizing channel p = 0.05 superop = tq.math.Superop.from_kraus( np.sqrt(1 - p) * tq.Gate.id.mat, np.sqrt(p / 3) * tq.Gate.x.mat, np.sqrt(p / 3) * tq.Gate.y.mat, np.sqrt(p / 3) * tq.Gate.z.mat, )
- Parameters:
*ops – One or more
array_likeKraus operators.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Returns:
The superoperator corresponding to the given set of Kraus operators.
- Return type:
- property kraus
The Kraus representation of this superoperator; see
from_kraus()for details about the representation. Note that Kraus representations are not unique, and this decomposition is only possible if the superoperator is CP (seeis_cp). The format is a 3-D arrayopsof shape(n_ops, dim, dim)whereops[i,:,:]is the \(i^{th}\) Kraus operator.Note
Although this attribute is not the underlying superoperator storage format, it is memoized when called, so that subsequent calls do not need to compute the value.
- Type:
numpy.ndarray
- plot_kraus(n_columns=4, abs_max=None, axes=None)
Plots a Kraus representation of this superoperator; see
from_kraus()for details about the representation. Note that Kraus representations are not unique.- Parameters:
n_columns (
int) – If new axes are made, how many columns of subplots to use.abs_max (
NoneType|float) – The value to scale absolute values of the matrix by; the value at which plotted colors become fully opaque. By default, this is the largest absolute magnitude of the input matrix.axes (
Iterable|NoneType) – An existing list of axes to plot on. They are created otherwise.
- static from_unitary(u, dim=None)
Instantiates a new
Superopfrom a given unitary matrix. A unitary matrix \(U\) acts on a given matrix by the formula \(\rho\mapsto U\rho U^\dagger\).import trueq as tq # instantiate a CNOT as a superoperator superop = tq.math.Superop.from_unitary(tq.Gate.cnot.mat)
- Parameters:
u (
numpy.ndarray) – A unitary matrix.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Returns:
The superoperator that conjugates input states by the given unitary matrix.
- Return type:
- static from_function(fcn, total_dim=None, dim=None)
Instantiates a new
Superopfrom a python function.import trueq as tq def depolarizing(rho, p=0.05): d = rho.shape[0] return (1 - p) * rho + p * np.eye(d) * np.trace(rho) / d # instantiate a qubit depolarizing channel superop = tq.math.Superop.from_function(depolarizing, 2) # instantiate a qutrit depolarizing channel superop = tq.math.Superop.from_function(depolarizing, 3)
Note
The function is assumed to be a linear function of a single density matrix. Passing a nonlinear function will result in a linear approximation that reproduces the action of the function on a basis of the operator space.
- Parameters:
fcn (
function) – A function that takes a density matrix and returns a density matrix of the same shape.total_dim (
int|NoneType) – The total Hilbert space dimension that this superoperator acts on. This will control the size of density matrix that is input intofcn. The default value ofNonewill result in the default dimension obtained fromget_dim().dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Returns:
The superoperator that maps a density matrix to the state returned by the given function.
- Return type:
- Raises:
ValueError – If
dimdoes not dividetotal_dim.
- from_qobj()
Instantiates a new
Superopfrom a QuTiP operator object.import qutip as qt import trueq as tq # make some QuTiP operator cx = qt.sigmax() # convert to a Superop and plot s = tq.math.Superop.from_qobj(cx) s.plot_ptm()
- Parameters:
qobj (
qutip.Qobj) – A QuTiP superoperator object.- Returns:
The superoperator for a given qobj.
- Return type:
- Raises:
RuntimeError – :If QuTiP is not imported.
ValueError – If the given qobj has non-uniform subsystem dimensions.
- property qobj
A new QuTiP superoperator object generated by this instance.
import qutip as qt import trueq as tq # construct a Superop from a simulation sim = tq.Simulator().add_stochastic_pauli(px=0.04).add_overrotation(0, 0.03) s = tq.math.Superop(sim.operator(tq.Cycle({(0, 1): tq.Gate.cx})).mat()) # convert to a Qobj and plot o = s.qobj qt.visualization.matrix_histogram_complex(o)
(<Figure size 640x480 with 2 Axes>, <Axes3D: >)
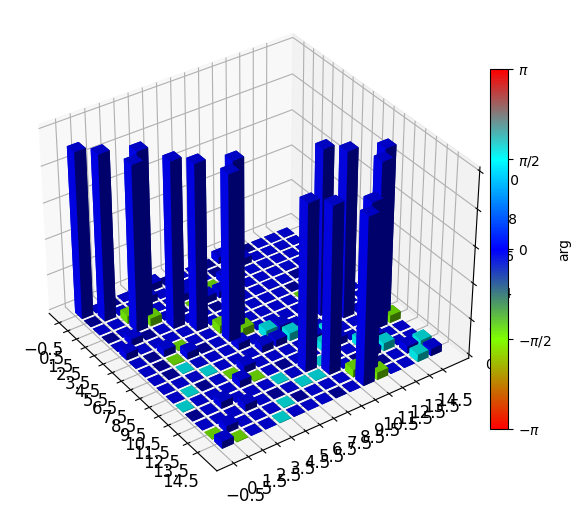
QuTiP is an optional dependency and must be installed for this function to work.
- Type:
qutip.Qobj- Raises:
RuntimeError – If QuTiP is not imported.
- static from_ptm(ptm)
Instantiates a new
Superopfrom a Pauli transfer matrix (PTM). A PTM represents how density matrices are transformed when expanded in the Pauli basis. In particular, suppose that for \(n\) qubits the Pauli matrices are denoted by \(\{P_i\}_{i=0}^{4^n-1}\), and sorted lexicographically. For example with \(n=2\), we have the ordering\[\{P_i\}_{i=0}^{15} =\{II, IX, IY, IZ, XI, XX, XY, XZ, YI, YX, YY, YZ, ZI, ZX, ZY, ZZ\}.\]Given any density matrix \(\rho\), we can expand it in the Pauli basis as \(\rho=\sum_{i=4^n-1} c_i P_i\). A PTM \(A\) performs the transformation \(c\mapsto A c\) where \(c\) is the vector \(c=(c_0,c_1,...,c_{4^n-1})\).
import numpy as np import trueq as tq # instantiate a qubit depolarizing channel superop = tq.math.Superop.from_ptm(np.diag([1, 0.99, 0.99, 0.99]))
The PTM can be generalized to subsystems with \(d>2\) using the Weyl operators, which are a set of \(d^2\) mutually orthogonal unitary matrices. However, unlike the Paulis, they are not generally Hermitian which leads to non-real elements of the PTM for CP (see
is_cp) maps. The expected order corresponds tolex=Falseinall.This representation is identical to
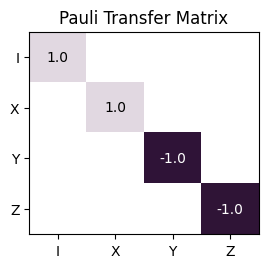
from_herm_ptmfor \(d=2\). For \(d>2\), this method differs fromfrom_herm_ptmonly in thatmatis used to create the representation basis instead ofherm_mat.import trueq as tq import matplotlib.pyplot as plt # plot ptm of the Z operator on the left, and herm_ptm on the right z = tq.math.Superop.from_unitary(tq.math.Weyls("W01", 3).mat) _, (ax1, ax2) = plt.subplots(1, 2, figsize=(9, 4)) z.plot_ptm(ax=ax1) z.plot_herm_ptm(ax=ax2)
- Parameters:
ptm (
numpy.ndarray) – A square matrix.- Returns:
The superoperator for a given PTM.
- Return type:
- Raises:
ValueError – If the PTM does not have a width that is an even power of a small prime number.
- property ptm
The Pauli transfer matrix representation of this superoperator; see
from_ptm()for details on this representation.- Type:
numpy.ndarray
- plot_ptm(abs_max=None, ax=None)
Plots the Pauli transfer matrix representation of this superoperator; see
from_ptm()for details on this representation.- Parameters:
abs_max (
NoneType|float) – The value to scale absolute values of the matrix by; the value at which plotted colors become fully opaque. By default, this is the largest absolute magnitude of the input matrix.ax (
matplotlib.Axis|NoneType) – An existing axis to plot on. One is created otherwise.
- static from_herm_ptm(ptm)
Instantiates a new
Superopfrom a Pauli transfer matrix (PTM). A PTM represents how density matrices are transformed when expanded in the Pauli basis. In particular, suppose that for \(n\) qubits the Pauli matrices are denoted by \(\{P_i\}_{i=0}^{4^n-1}\), and sorted lexicographically. For example with \(n=2\), we have the ordering\[\{P_i\}_{i=0}^{15} =\{II, IX, IY, IZ, XI, XX, XY, XZ, YI, YX, YY, YZ, ZI, ZX, ZY, ZZ\}.\]Given any density matrix \(\rho\), we can expand it in the Pauli basis as \(\rho=\sum_{i=4^n-1} c_i P_i\). A PTM \(A\) performs the transformation \(c\mapsto A c\) where \(c\) is the vector \(c=(c_0,c_1,...,c_{4^n-1})\).
import numpy as np import trueq as tq # instantiate a qubit depolarizing channel superop = tq.math.Superop.from_ptm(np.diag([1, 0.99, 0.99, 0.99]))
The PTM can be generalized to subsystems with \(d>2\) using the Weyl operators, which are a set of \(d^2\) mutually orthogonal unitary matrices. However, unlike the Paulis, they are not generally Hermitian which would lead to non-real elements of the PTM for CP (see
is_cp) maps. Therefore, we use a symmetrized version of the Weyl matrices,herm_matfor details. The expected order corresponds tolex=Falseinall.This representation is identical to
from_ptmfor \(d=2\). For \(d>2\), this method differs fromfrom_ptmonly in thatherm_matis used to create the representation basis instead ofmat.import trueq as tq import matplotlib.pyplot as plt # plot ptm of the Z operator on the left, and herm_ptm on the right z = tq.math.Superop.from_unitary(tq.math.Weyls("W01", 3).mat) _, (ax1, ax2) = plt.subplots(1, 2, figsize=(9, 4)) z.plot_ptm(ax=ax1) z.plot_herm_ptm(ax=ax2)
- Parameters:
ptm (
numpy.ndarray) – A square matrix.- Returns:
The superoperator for a given PTM.
- Return type:
- Raises:
ValueError – If the PTM does not have a width that is an even power of a small prime number.
- property herm_ptm
The Pauli transfer matrix representation of this superoperator; see
from_ptm()for details on this representation.- Type:
numpy.ndarray
- plot_herm_ptm(abs_max=None, ax=None)
Plots the Pauli transfer matrix representation of this superoperator; see
from_ptm()for details on this representation.- Parameters:
abs_max (
NoneType|float) – The value to scale absolute values of the matrix by; the value at which plotted colors become fully opaque. By default, this is the largest absolute magnitude of the input matrix.ax (
matplotlib.Axis|NoneType) – An existing axis to plot on. One is created otherwise.
- static from_choi(choi, dim=None)
Instantiates a new
Superopfrom a Choi matrix. If a channel \(\Lambda\) transforms a given density matrix as \(\rho\mapsto \Lambda(\rho)\), then the Choi matrix (in the row convention) is equal to \(\Lambda_r=\sum_{i,j=0}^{d-1}\Lambda(E_{i,j})\otimes E_{i,j}\) where \(d\) is the dimension, and \(E_{i,j}\) is the \(d\times d\) matrix of zeros with a 1 in the \((i,j)^\text{th}\) entry.The Choi matrix is positive semidefinite if and only if the superoperator it represents is completely positive (see
is_cp). Therefore, there is a correspondence between completely positive superoperators and density matrices (which must also be positive semidefinite) that is often called the Choi-Jamiolkowski isomorphism.import numpy as np import trueq as tq # instantiate a random CP qubit channel superop = tq.math.Superop.from_choi(2 * tq.math.random_density(4))
- Parameters:
choi (
numpy.ndarray) – A Choi matrix.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Returns:
The superoperator for a given Choi matrix.
- Return type:
- property choi
The Choi matrix representation of this superoperator; see
from_choi()for details on this representation.- Type:
numpy.ndarray
- plot_choi(abs_max=None, ax=None)
Plots the Choi representation of this superoperator; see
from_choi()for details on this representation.- Parameters:
abs_max (
NoneType|float) – The value to scale absolute values of the matrix by; the value at which plotted colors become fully opaque. By default, this is the largest absolute magnitude of the input matrix.ax (
matplotlib.Axis|NoneType) – An existing axis to plot on. If omitted, a new one is created.
- static from_rowstack(mat, dim=None)
Instantiates a new
Superopfrom a Liouville superoperator matrix in the row-stacking basis. Note that since this is the native basis of theSuperopclass, this method is equivalent to the constructor.This is the best representation for superopertors for simulation if density matrices are C-ordered (i.e. row-major, so that entire rows are contiguous in memory). This is because if our row-stacking superoperator matrix is \(M\) and our density matrix \(\rho\), then if we take the rows of \(\rho\) and stack them together into one column vector, denoted \(\operatorname{vec}(\rho)\), then the output density matrix is given by regular matrix multiplication, \(\operatorname{vec}^{-1}(M\operatorname{vec}(\rho))\), where \(\operatorname{vec}^{-1}\) is the unstacking operator.
import numpy as np import trueq as tq # instantiate the identity channel on a qutrit superop = tq.math.Superop.from_rowstack(np.eye(9))
- Parameters:
mat (
numpy.ndarray) – A superoperator in the row-stacking basis.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Return type:
- property rowstack
The matrix representation of this superoperator in the row-stacking basis; see
from_rowstack()for details on this representation.- Type:
numpy.ndarray
- plot_rowstack(abs_max=None, ax=None)
Plots the matrix representation of this superoperator in the row-stacking basis; see
from_rowstack()for details on this representation.- Parameters:
abs_max (
NoneType|float) – The value to scale absolute values of the matrix by; the value at which plotted colors become fully opaque. By default, this is the largest absolute magnitude of the input matrix.ax (
matplotlib.Axis|NoneType) – An existing axis to plot on. If omitted, a new one is created.
- static from_rowstack_subsys(mat, dim=None)
Instantiates a new
Superopfrom a Liouville superoperator matrix in the row-stacking subsystem-wise basis. If a unitary \(U=U_1\otimes U_2\) acts on some bipartite Hilbert space, thenrowstack(which is also the native representation used by this class) is equal to\[U\otimes \overline{U} =U_1 \otimes U_2 \otimes \overline{U}_1 \otimes \overline{U}_2\]which we call the global rowstacking convention. It is sometimes more useful to use the subsystem-wise rowstacking convention where the wires of each subsystem are grouped together, corresponding to the unitary
\[U\otimes \overline{U} =U_1 \otimes \overline{U}_1 \otimes U_2 \otimes \overline{U}_2\]Indeed, this is the convention used by
OperatorTensorand hence also by theSimulator. This idea generalizes to n-partite superoperators.import numpy as np import trueq as tq # instantiate the identity channel on two qubits superop = tq.math.Superop.from_rowstack_subsys(np.eye(16))
- Parameters:
mat (
numpy.ndarray) – A superoperator in the row-stacking subsystem-wise basis.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Return type:
- property rowstack_subsys
The matrix representation of this superoperator in the row-stacking basis; see
from_rowstack_subsys()for details on this representation.Note
Although this attribute is not the underlying superoperator storage format, it is memoized when called, so that subsequent calls do not need to compute the value.
- Type:
numpy.ndarray
- plot_rowstack_subsys(abs_max=None, ax=None)
Plots the matrix representation of this superoperator in the row-stacking subsystem-wise basis; see
from_rowstack_subsys()for details on this representation.- Parameters:
dim (
int) – The dimension of each Hilbert space subsystem, e.g. 2 for qubits.abs_max (
NoneType|float) – The value to scale absolute values of the matrix by; the value at which plotted colors become fully opaque. By default, this is the largest absolute magnitude of the input matrix.ax (
matplotlib.Axis|NoneType) – An existing axis to plot on. If omitted, a new one is created.
- static from_colstack(mat, dim=None)
Instantiates a new
Superopfrom a superoperator in the column-stacking basis.This is the best representation for superopertors for simulation if density matrices are Fortran-ordered (i.e. column-major, so that entire columns are contiguous in memory). This is because if our column-stacking superoperator matrix is \(M\) and our density matrix \(\rho\), then if we take the columns of \(\rho\) and stack them together into one column vector, denoted \(\operatorname{vec}(\rho)\), then the output density matrix is given by regular matrix multiplication, \(\operatorname{vec}^{-1}(M\operatorname{vec}(\rho))\), where \(\operatorname{vec}^{-1}\) is the unstacking operator.
import numpy as np import trueq as tq # instantiate the identity channel on a qutrit superop = tq.math.Superop.from_colstack(np.eye(9))
- Parameters:
mat (
numpy.ndarray) – A superoperator in the column-stacking basis.dim (
int|NoneType) – The dimension of each subsystem this superoperator acts on, e.g.2for qubits. IfNone, the constructor will try to automatically infer the subsystem dimension by usingauto_base().
- Return type:
- property colstack
The matrix representation of this superoperator in the column-stacking basis; see
from_colstack()for details on this representation.- Type:
numpy.ndarray
- plot_colstack(abs_max=None, ax=None)
Plots the matrix representation of this superoperator in the col-stacking basis; see
from_colstack()for details on this representation.- Parameters:
abs_max (
NoneType|float) – The value to scale absolute values of the matrix by; the value at which plotted colors become fully opaque. By default, this is the largest absolute magnitude of the input matrix.ax (
matplotlib.Axis|NoneType) – An existing axis to plot on. If omitted, a new one is created.
- property lkpd
The leading Kraus polar decomposition (LKPD) of this superoperator. This is a tuple
u, pwhereuis unitary andpis positive semi-definite, and the productu @ pis equal to the leading Kraus term.See [8] for a comprehensive overview of this form. In short, when eigenvectors of a positive semi-definite Choi matrix are scaled by the square-roots of their eigenvalues and devectorized into square matrices, they form a set of mutually orthogonal Kraus operators for the channel. The Kraus operator corresponding to the largest eigenvalue forms a convenient approximation to the channel when the channel is nearly unitary. The QR decomposition of this leading Kraus term separates leading dynamics of the channel into unitary and stochastic behaviour.
Note
This is a partial representation because it does not contain all information about the superoperator; non-leading terms of the Kraus representation are dropped.
- Type:
tuple
- plot_lkpd(axes=None, abs_max=None)
Plots both matrices of the polar decomposition of the leading Kraus term of this superoperator; see
lkpd()for details on this (partial) representation.- Parameters:
abs_max (
NoneType|float) – The value to scale absolute values of the matrix by; the value at which plotted colors become fully opaque. By default, this is the largest absolute magnitude of the input matrix.axes (
Iterable|NoneType) – An existing list of axes to plot on. They are created otherwise.
- apply(state)
Applies this superoperator to a given density matrix or pure state. The output is always a density matrix of shape
(dim, dim).import numpy as np import trueq as tq # make a superoperator acting on a qutrit s = tqm.Superop.random_constrained_cptp(3, 0.01, 0.4) # apply to a pure state s.apply([1, 0, 0])
array([[ 0.99109831+2.35704703e-21j, -0.04875147-1.74607736e-02j, -0.00666083-3.99938500e-02j], [-0.04875147+1.74607736e-02j, 0.00552156+4.85759556e-22j, 0.001326 +2.24434193e-03j], [-0.00666083+3.99938500e-02j, 0.001326 -2.24434193e-03j, 0.00338014-6.75597438e-21j]])- Parameters:
state (
numpy.ndarray-like) – An input density matrix or pure state of the correct shape.- Returns:
The image of state under this superoperator.
- Return type:
numpy.ndarray
Tensors
- class trueq.math.tensor.Tensor(output_shape, input_shape=None, spawn=None, value=None, dtype=None)
Represents a multipartite tensor on an arbitrary number of subsystems. Each subsystem owns a number of ordered wires (or indices), which can each be input or output wires (e.g., lower and upper indices in Einstein’s notation). One important restriction is that all subsystems have the same wire description: the same number, dimensions, and order for input and output wires.
Here are some motivating cases for various output and input shapes
output, input:(d,), (): Pure states on a multipartite qubit system. Each subsystem has a single output wire of dimension \(d\) and no input wires (i.e., a column vector). SeeStateTensor.(d,), (): Probability distributions over Cartesian products of dits. Each subsystem has a single output wire of dimension \(d\) and no input wires (i.e., a column vector).(d,d), (): Vectorized mixed states on a multipartite qubit system. Each subsystem has two output wires each with dimension \(d\) and no input wires. The first output wire represents the output wire of the unvectorized state, and the second output wire the input wire of the unvectorized state (this is the row-stacking convention). SeeStateTensor.(d,), (d,): Unitaries acting on a multipartite qubit system. Each subsystem has a single output wire of dimension \(d\) and a single input wire of dimension \(d\) (i.e., a square matrix). SeeOperatorTensor.(d,d), (d,d): Superoperators acting on a multipartite qubit system. Each subsystem has two input wires and two output wires, all of dimension \(d\). The two input wires act on a vectorized density matrix (or contract against another superoperator in composition). SeeOperatorTensor.
A main feature of this class is the ability to efficiently left-multiply square matrices onto specific subsystems (see
apply_matrix()), which can be strictly smaller than all of the subsystems present in the tensor. Therefore this class can be used to maintain the state of a simulation, and is general enough to track pure states, mixed states, unitaries, and superoperators.import trueq as tq import numpy as np t = tq.math.Tensor(2, 2, spawn=np.eye(2)) t.apply_matrix((0, 2), tq.Gate.cnot.mat) t.apply_matrix((1,), tq.Gate.h.mat) # display the matrix corresponding to the circuit {(0, 2): cnot, (1,): h} tq.plot_mat(t.mat().reshape(8, 8))
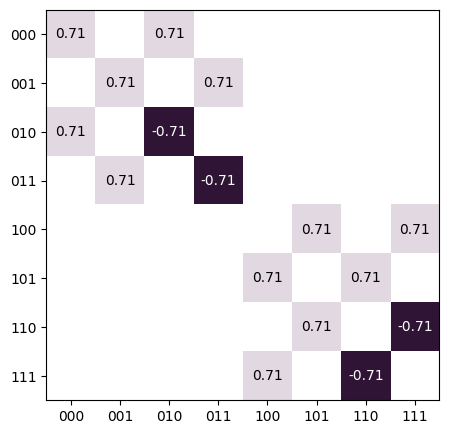
The internal storage format of this class is a dictionary mapping labels to NumPy arrays, such as the following:
{ (0,): [[0, 1], [1, 0]], (2, 3): [[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 0, 1], [0, 0, 1, 0]], }
{(0,): [[0, 1], [1, 0]], (2, 3): [[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 0, 1], [0, 0, 1, 0]]}In the above example, the label
(0,)stores an X gate, and the labels(2, 3)store a CNOT gate.- Parameters:
output_shape (
tuple|int) – The output wire dimension, or a tuple of output wire dimensions. Set to an empty tuple for no output wires.input_shape (
tuple|int|NoneType) – The input wire dimension, or a tuple of input wire dimensions. Set to an empty tuple orNonefor no input wires.spawn (
numpy.ndarray-like) – The default value to assign to new subsystems. The size must match the provided input and output shapes. By default, this parameter is set to the tensor of all zeros, except the first element, which is 1.value (
dict) – The initial value of the tensor, set as a dictionary mapping tuples of subsystem indexes to tensors of the correct shape.dtype – The data type of the arrays,
numpy.float64by default.
- property dtype
The data type of this tensor.
- Type:
type
- property labels
Which subsystem labels of this tensor have a value.
- Type:
tuple
- property n_sys
The number of subsystem labels with a value
- Type:
int
- property shape
The output and input shape of each subsystem, e.g.,
((2, 2), (2, 2)). See the argumentsinput_shapeandoutput_shapeof the constructor ofTensor.- Type:
tuple
- property total_dim
The total dimension of this tensor; the total subsystem dimension to the power of the number of subsystems.
- Type:
int
- property spawn
The array that is assigned to new subsystems by default.
- Type:
numpy.ndarray
- conj(copy=True)
Takes the complex conjugate of each array in this tensor.
- Parameters:
copy (
bool) – Whether to mutate the given tensor, or to create a copy and leave the original intact.- Returns:
This instance or a copy.
- Return type:
- adj(copy=True)
Takes the complex conjugate and transpose of each array in this tensor. Here, transpose refers to swapping the input shape with the output shape.
- Parameters:
copy (
bool) – Whether to mutate the given tensor, or to create a copy and leave the original intact.- Returns:
This instance or a copy.
- Return type:
- transpose(output_perm, input_perm, copy=True)
Permutes wire dimensions of this tensor, possibly switching input wires with output wires.
from trueq.math import Tensor # turn a column vector into a row vector t = Tensor((2,)) print(t.shape, t.transpose([], [0]).shape) # vectorize a matrix with row-stacking t = Tensor((2,), (2,)) print(t.shape, t.transpose([0, 1], []).shape) # vectorize a matrix with column-stacking t = Tensor((2,), (3,)) print(t.shape, t.transpose([1, 0], []).shape) # shuffle some wires t = Tensor((2, 3), (5,)) print(t.shape, t.transpose([2, 1], [0]).shape)
((2,), ()) ((), (2,)) ((2,), (2,)) ((2, 2), ()) ((2,), (3,)) ((3, 2), ()) ((2, 3), (5,)) ((5, 3), (2,))
- Parameters:
output_perm (
Iterable) – A list of indices referencing positions in the joint tupleshape = output_shape + input_shape. Thereforeoutput_perm + input_permmust be a permutation ofrange(len(shape)).input_perm (
Iterable) – A list of indices referencing positions in the joint tupleoutput_shape + input_shape.copy (
bool) – Whether to mutate the given tensor, or to create a copy and leave the original intact.
- Returns:
This instance or a copy.
- Return type:
- value(order='subsystem')
Returns the value of this tensor: a dictionary mapping tuples of subsystem labels to array values.
The argument of this method changes the order of indexes of the arrays. For simulation performance reasons, the internal storage arranges them subsystem-wise, so that all input wires for a given subsystem are contiguous, and likewise all output wires for a given subsystem are contiguous, and this is the default order of this method. This can optionally be changed so that indices are riffled over subsystems.
As an example, suppose the input shape is
(2, 4)and the output shape is(5,)and that there are 3 subsystems in an array. Then the array will have shape(2, 4, 2, 4, 2, 4, 5, 5, 5)if the order is"subsystem"(default), or the array will have shape(2, 2, 2, 4, 4, 4, 5, 5, 5)if the order is"composite".As a convenience, appending
"-flat"to the order flattens all inputs and all outputs separately, giving a shape(512, 125)in this example, whether the order is composite or subsystem based. Further, appending"-group"to composite order flattens each group of subsystems, giving a shape(8, 64, 125)in this example.- Parameters:
order (
str) – Which order to arrange the wires, either"subsystem","subsystem-flat","composite","composite-group", or"composite-flat". Or, one of"s","sf","c","cg", or"cf"for short.- Return type:
dict
- mat(order='subsystem', labels=None)
Returns the full matrix representation of this tensor, with subsystems ordered by sorted labels.
Note
Note that this property will create an array that is exponentially large in the number of subsystems, and causes any distinct subsystems found in
value()to be permanently merged; calling this attribute mutates the tensor’s internal representation.- Parameters:
order (
str) – Advanced users seeTensor.value().labels (
Iterable) – The desired subsystem label order, which must be a permutation oflabels. By default, labels are ordered from smallest to biggest.
- Return type:
numpy.ndarray
- add_labels(labels)
Updates the number of subsystems to include labels provided, if they do not already exist. If the labels are already present, this call doesn’t change anything.
- Parameters:
labels (
Iterable) – A list of labels to be added to this tensor.- Returns:
This instance.
- Return type:
- merge(labels)
Merges the given labels together after adding any labels that are not already present.
- Parameters:
labels (
Iterable) – A list of labels.- Returns:
An unsorted tuple containing all of the labels in the partite resulting from this merge.
- Return type:
tuple
- upgrade()
Does nothing. This is to be used by subclasses that require a mutation of shape on a call to
marginalize(). See, for instance,StateTensor.upgrade()andOperatorTensor.upgrade().- Returns:
This instance.
- Return type:
- marginalize(labels, assume_unital=True, copy=True)
Keeps the provided labels of this tensor by marginalizing the remaining labels. Here, marginalization is defined as the sum over all tensor indices of the remaining labels.
import trueq as tq import numpy as np # Make a random probability distribution on length-4 bitstrings s = tq.settings.get_rng().random(16) p = tq.math.Tensor(2, value={(0, 1, 2, 3): s / s.sum()}) # Keep two of the bitstrings and marginalize the rest p.marginalize((1, 2))
Tensor(<[(2,), ()] on labels [(1, 2)]>)
- Parameters:
labels (
tuple) – Which labels to keep. The order does not matter.assume_unital (
bool) – Assumes that each factor in the tensor has a sum of 1. Otherwise, in the case where entire entries invalue()need to be removed, sums are still computed and multiplied onto some other entry so that the overall sum of the tensor is preserved. In the case where all labels in the tensor are marginalized, label(0,)is re-added so that the total sum of the tensor can be preserved.copy (
bool) – Whether to make a copy of this tensor, or mutate it in place.
- Returns:
This instance.
- Return type:
- update(other)
Updates this tensor with some new values. If values are placed on labels that do not exist, creates and sets them. If values are placed on labels that already exist, they are first removed by calling
marginalize().
- apply_matrix(labels, matrix)
Mutates this tensor by applying the given square matrix to the given labels.
The size of the matrix must be compatible with the output shape of this tensor; just as with regular matrix multiplication, \(AB\), the number of columns of \(A\) must match the number of rows of \(B\). The rule enforced here is that the number of rows of the given matrix, when reshaped into a square, must be equal to the product of this tensor’s output wire dimensions. Square matrices are enforced to avoid changing the shape of the tensor.
import trueq as tq import numpy as np rng = tq.settings.get_rng() t = tq.math.Tensor((2, 3), (2,)) # we need a 6x6 since output shape is (2, 3) t.apply_matrix((0,), rng.standard_normal((6, 6))) # we need a 36x36 since we are applying to 2 systems t.apply_matrix((0, 3), rng.standard_normal((36, 36)))
(0, 3)
- Parameters:
labels (
Iterable) – Which subsystems to apply the matrix to.matrix (
numpy.ndarray-like) – A square matrix.
- Returns:
The labels to which the matrix was applied, including labels that needed to be merged together.
- Return type:
tuple
- apply_to_all(mat, copy=False)
Applies a matrix to every subsystem of this tensor.
- Parameters:
mat (
numpy.ndarray) – A matrix to apply to this system, which must be square ifcopy == False.copy (
bool) – Whether to make a copy of this tensor, or mutate it in place.
- Returns:
This instance, or the copied instance.
- Return type:
- apply_ufunc(ufunc)
Applies a NumPy universal function to every array in this tensor.
- Parameters:
ufunc (
numpy.ufunc) – A universal function to apply to every array.
- dot(rhs, dtype=None, overwrite_rhs=False)
Contracts this tensor with another tensor, returning a new tensor. The only shape restriction is that this tensor’s input shape must match the output tensor’s output shape. The returned tensor has input-output shapes
(this.output_shape, rhs.input_shape); the inner shapes have been contracted against each other.import trueq.math as tqm import numpy as np rng = np.random.default_rng() lhs = tqm.Tensor(5, (2, 3), value={(0, 1): rng.standard_normal((25, 36))}) rhs = tqm.Tensor((2, 3), 4, value={(1, 5): rng.standard_normal((36, 16))}) product = lhs.dot(rhs) print(product.shape) print(product.labels)
((5,), (4,)) (0, 1, 5)
- Parameters:
rhs (
Tensor) – Another tensor with a compatible shape.dtype (
numpy.dtype) – The data type of the output tensor. If either of the inputs are complex, and the output is real, the real part is taken without warning.overwrite_rhs (
bool) – Whether to mutaterhsso that its final value is the product. Otherwise, a copy ofrhsis made.
- Return type:
- sample(n_shots=1, labels=None)
Assumes that this tensor represents a categorical probability distribution over ditstrings and samples
n_shotsfrom it, or a marginalized version of it iflabelsare provided.import trueq.math as tqm probs = tqm.Tensor(2, value={(0,): [0, 1], (1, 2): [0, 0.5, 0, 0.5]}) probs.sample(100) # Results({"101": 52, "111": 48}) probs.sample(100, labels=(0, 2)) # Results({"11": 100})
Results({'11': 100})- Parameters:
n_shots (
int) – The number of samples to draw from the distribution.labels (
Iterable) – A list of labels to sample from.
- Return type:
- to_results(labels=None, clip=True)
Constructs a new
Resultsobject whose ditstring values are equal to the corresponding matrix entries of this tensor.import trueq.math as tqm probs = tqm.Tensor(2, value={(1,): [0, 1], (0, 2): [0, 0.5, 0, 0.5]}) probs.to_results()
Results({'011': 0.5, '111': 0.5})- Parameters:
labels (
Iterable) – A list of labels to slice, in case a subset of all labels present in this tensor is desired. IfNone, all labels present in the tensor are used (in sorted order).clip (
bool) – Whether or not to clip the values to the interval \([0, 1]\).
- Return type:
- class trueq.math.tensor.StateTensor(dim=None, spawn=None, value=None)
Represents a pure or mixed state on a multipartite qubit system. This is one of the main output formats of the
Simulator. It differs from just a pure matrix, such as anumpy.ndarray, in that it also stores qubit label information, and attempts to store a sparse representation when the state is not entangled between various subsystems.Depending on the types of noise in your simulator, this state could be pure or mixed. This will affect the dimension. You can check which case you have with
is_mixed. You can get the matrix representation withmat().import trueq as tq # construct a circuit that makes a 3-qubit cat state circuit = tq.Circuit() circuit.append({(0,): tq.Gate.h}) circuit.append({(0, 1): tq.Gate.cnot}) circuit.append({(1, 2): tq.Gate.cnot}) # use a simulator to fetch the state of this circuit as a StateTensor state = tq.Simulator().state(circuit) # print the 1D pure state vector print(state.mat()) # get the density matrix representation state.upgrade() tq.plot_mat(state.mat())
[0.70710678+0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0.70710678+0.j]
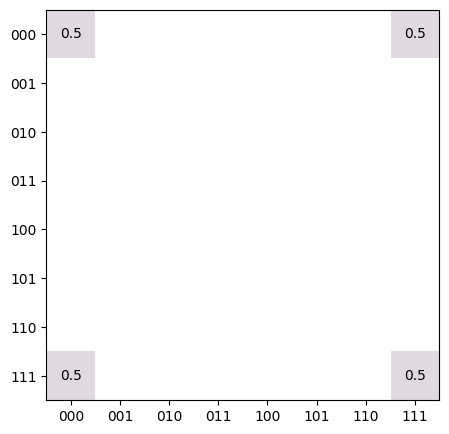
What follows is information intended for users that want to do a bit more than get the matrix representation of a state. This class has a few main distinctions from its parent class
Tensor:The datatype is always
numpy.complex128.The
mat()andvalue()methods return a more convenient tensor order and shape by default.The
upgrade()method, which transforms this state from a pure state into a mixed state by taking appropriate outer products and changing the output shape from(d,)to(d,d). Certain methods automatically callupgrade(), for example, when a superoperator-shaped matrix is given toapply_matrix().Certain functions like
marginalizehave been special-cased to quantum states.
import trueq as tq import numpy as np # make a pure state on a tensor product of qubits psi = tq.math.StateTensor(2) # we can manually upgrade it to a mixed state rho = psi.upgrade() # or we can automatically upgrade it to a mixed state by doing something that # requires a mixed state. here, we apply something of superoperator size, rather # than unitary size psi = tq.math.StateTensor(2) psi.apply_matrix((0,), np.eye(4)) # we can also create a mixed state on instatiation based on spawn/value shapes rho = tq.math.StateTensor(2, spawn=[[1, 0], [0, 0]])
Note
This class does not assume that the represented state is positive or that it has unit trace, or that applied operators are unitary, CP , TP, unital, etc.: it just stores and manipulates complex numerical arrays.
- Parameters:
dim (
int|NoneType) – The Hilbert space dimension of a single subsystem. The default value ofNonewill result in the default dimension obtained fromget_dim().spawn (
numpy.ndarray-like) – The default state to set a subsystem to when its label is refered to, but it does not exist yet. This spawn can be pure or mixed. See also the constructor ofTensor.value (
dict) – The initial value of this state, which can either be pure or mixed. See also the constructor ofTensor.
- property is_mixed
Whether this state currently is a mixed state (as opposed to a pure state). Equivalent to
is_upgraded.- Type:
bool
- property is_upgraded
Whether this state currently is a mixed state (as opposed to a pure state). Equivalent to
is_mixed.- Type:
bool
- property dim
The Hilbert space dimension of the subsystems of this state.
- Type:
int
- upgrade()
If this state represents a pure state, upgrades it to a mixed state by taking outer products. If this state is already a mixed state, does nothing.
- Returns:
This instance.
- Return type:
- value(order='composite-group')
Returns a dictionary mapping tuples of subsystem labels to states on those subsystems. If this state is currently pure, then states will be 1D vectors, and if mixed, then states will be 2D density matrices.
- Parameters:
order (
str) – Advanced users seeTensor.value().- Return type:
dict
- mat(order='composite-group', labels=None)
If this state is currently pure, returns the pure state vector, otherwise returns the density matrix.
Note
Note that this property will create an array that is exponentially large in the number of subsystems, and causes any distinct subsystems found in
value()to be permanently merged; calling this attribute mutates the tensor’s internal representation.- Parameters:
order (
str) – Advanced users seeTensor.value().labels (
Iterable) – The desired subsystem label order, which must be a permutation oflabels. By default, labels are ordered from smallest to biggest.
- Return type:
numpy.ndarray
- apply_matrix(labels, matrix)
Mutates this state by applying the given square matrix to the given labels.
If acting on \(n\) subsystems, this matrix can be a \(d^n \times d^n\) unitary, or a \(d^{2n}\times d^{2n}\) superoparator. If this state is currently pure and a superoperator is applied,
upgrade()is called. If this state is currently mixed and a unitary is applied, the unitary is made into a superoperator before applying.import trueq as tq import numpy as np t = tq.math.StateTensor(2) # apply a 2-qubit unitary t.apply_matrix((0, 1), tq.Gate.cnot.mat) # apply a 1% bitflip superoperator to qubit 1. This upgrades to mixed state s = 0.99 * np.eye(4) + 0.01 * np.kron(tq.Gate.x.mat, tq.Gate.x.mat) t.apply_matrix((1,), s) # display the final mixed state tq.plot_mat(t.mat())
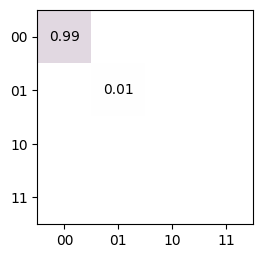
The vectorization convention of superoperators is important. Mixed states are stored in a subsystem-wise row-stacked vectorization convention, and therefore superoperators need to use this convention too. See
to_rowstack_super().- Parameters:
labels (
Iterable) – Which subsystems to apply the matrix to.matrix (
numpy.ndarray-like) – A square matrix.
- marginalize(labels, assume_unital=False, copy=False)
Keeps the provided labels of this tensor by taking the partial trace of the remaining labels. This will usually
upgrade()a pure state to a mixed state.The special case of no upgrade happens when this state is pure and all the labels being traced out are known to be unentangled with other labels (this is known when every label tuple in the keys of
value()is either a strict subset of the given labels, or does not intersect at all with the given labels).- Parameters:
labels (
tuple) – Which labels to keep. The order does not matter.assume_unital (
bool) – Assumes that each factor in the tensor has a trace of 1. Otherwise, in the case where entire entries invalue()need to be removed, traces are still computed and multiplied onto some other entry so that the overall trace of the tensor is preserved. In the case where all labels in the tensor are traced out, label(0,)is re-added so that the total trace of the tensor can be preserved.copy (
bool) – Whether to make a copy of this tensor, or mutate it in place.
- Returns:
This instance.
- Return type:
- probabilities(povm=None)
Computes the probabilities of all possible measurement outcomes. A Positive Operator Valued Measurement (POVM), if provided, defines the measurement outcomes. Otherwise, the outcomes are computational basis measurements.
import trueq.math as tqm import numpy as np # compute probability distribution of a qubit superposition psi = tqm.StateTensor(2, value={(0,): np.array([1, -1j]) / np.sqrt(2)}) print(psi.probabilities().value()) # define a POVM corresponding to readout error that has a 1% chance of # flipping a |0> measurement and a 10% chance of flipping a |1> measurement p00 = 0.99 p11 = 0.9 povm = [[[p00, 0], [0, 1 - p11]], [[1 - p00, 0], [0, p11]]] povm = tqm.Tensor((2,), (2, 2), spawn=povm) print(psi.probabilities(povm).value()) # a more efficient implementation of the above, using a stochastic confusion # matrix instead of quantum measurement operators povm = tqm.Tensor(2, 2, spawn=[[p00, 1 - p11], [1 - p00, p11]]) print(psi.probabilities(povm).value())
{(0,): array([0.5, 0.5])} {(0,): array([0.545, 0.455])} {(0,): array([0.545, 0.455])}- Parameters:
povm (
Tensor) – ATensorwith shape((k,), (d, d))or((k,), (d,))wheredis the Hilbert space dimension, and(k,)is the number of possible outcomes per subsystem. In the former case, each slice[i,:,:]should be a positive matrix representing a measurement operator, and the sum overishould be the identity matrix to be probability preserving. In the latter case, the tensor represents a confusion matrix with which to modify the computational basis probabilities, and the sum of each row should be one to be probability preserving.- Return type:
dict
- class trueq.math.tensor.OperatorTensor(dim=None, spawn=None, value=None, dtype=None)
Represents an operator (e.g., unitary) or superoperator (e.g., CPTP channel) on a multipartite qubit system. This is one of the main output formats of the
Simulator. It differs from just a pure matrix, such as anumpy.ndarray, in that it also stores qubit label information, and attempts to store a sparse representation when the operator is not entangling between various subsystems.Depending on the types of noise in your simulator, this operator could be a unitary or a superoperator. This will affect the dimension. You can check which case you have with
is_superop. You can get the matrix representation withmat().import trueq as tq # construct a circuit that makes a 3-qubit cat state circuit = tq.Circuit() circuit.append({(0,): tq.Gate.h}) circuit.append({(0, 1): tq.Gate.cnot}) circuit.append({(1, 2): tq.Gate.cnot}) # use a simulator to fetch the unitary of this circuit as an OperatorTensor op = tq.Simulator().operator(circuit) # display the unitary matrix itself tq.plot_mat(op.mat())
What follows is information intended for users that want to do a bit more than get the matrix representation of an operator. This class has a few distinctions from its parent class
Tensor:The datatype is
numpy.complex128by default.The
mat()andvalue()methods return a more convenient tensor order and shape by default.The
upgrade()method, which transforms this operator into a superoperator mixed state by taking appropriate kroneckers and changing the input and output shapes from(d,)to(d,d). Certain methods automatically callupgrade(), for example, when a superoperator shaped matrix is given toapply_matrix().Certain functions like
marginalizehave been special-cased to quantum operators.
import trueq as tq import numpy as np # make a unitary channel for a tensor product of qubits psi = tq.math.OperatorTensor(2) # we can manually upgrade it to a superoperator rho = psi.upgrade() # or we can automatically upgrade it to a superoperator by doing something that # requires a superoperator. here, we apply something of superoperator size, # rather than unitary size psi = tq.math.OperatorTensor(2) psi.apply_matrix((0,), np.eye(4)) # we can also create superoperators on instantiation based on spawn/value shapes rho = tq.math.OperatorTensor(2, spawn=np.eye(4))
Note
This class does not assume that the represented channel or anything applied to it is unitary, CP, TP, unital, etc.: it is just stores and manipulates numerical arrays.
- Parameters:
dim (
int|NoneType) – The Hilbert space dimension of a single subsystem. The default value ofNonewill result in the default dimension obtained fromget_dim().spawn (
numpy.ndarray-like) – The default operator to set a subsystem to when its label is referred to, but it does not exist yet. This spawn can be operator or superoperator. See also the constructorTensor.value (
dict) – The initial value of this state, which can either be an operator or a superoperator. See also the constructor ofTensor.dtype (
type) – The datatype of this operator.
- property is_superop
Whether this tensor represents a superoperator (as opposed to a unitary).
- Type:
bool
- property is_upgraded
Whether this tensor represents a superoperator (as opposed to a unitary). Equivalent to
is_superop.- Type:
bool
- property dim
The Hilbert space dimension that subsystems of this state act on.
- Type:
int
- marginalize(labels, assume_unital=False, copy=False)
Keeps the provided labels of this tensor by taking the partial trace of the remaining labels. This will usually
upgrade()a unitary tensor into a superoperator tensor.The special case of no upgrade happens when this state is pure and all the labels being traced out are known to be unentangled with other labels (this is known when every label tuple in the keys of
value()is either a strict subset of the given labels, or does not intersect at all with the given labels).- Parameters:
labels (
tuple) – Which labels to keep. The order does not matter.assume_unital (
bool) – Assumes that each factor in the tensor has a trace of 1. Otherwise, in the case where entire entries invalue()need to be removed, traces are still computed and multiplied onto some other entry so that the overall trace of the tensor is preserved. In the case where all labels in the tensor are traced out, label(0,)is re-added so that the total trace of the tensor can be preserved.copy (
bool) – Whether to make a copy of this tensor, or mutate it in place.
- Returns:
This instance.
- Return type:
- upgrade()
If this operator represents a unitary, upgrades it to a tensor representing a superoperator. If this tensor already represents a superoperator, does nothing.
- Returns:
This instance.
- Return type:
- value(order='composite-flat')
Returns a dictionary mapping tuples of subsystem labels to operators on those subsystems. Operators acting on
nsubsystems will have shape(d**n,d**n)or(d**(2*n),d**(2*n))depending on the current value ofis_superop.- Parameters:
order (
str) – Advanced users seeTensor.value().- Return type:
dict
- mat(order='composite-flat', labels=None)
Returns the matrix form of this operator. The tensor order is the sorted list of all present labels. If
nsubsystems are present, this matrix will have shape(d**n,d**n)or(d**(2*n),d**(2*n))depending on the current value ofis_superop.If this is a superoperator, then the basis used is the composite row-stacking basis.
Note
Calling this method will create an array that is exponentially large in the number of subsystems, and causes any distinct subsystems found in
valueto be permanently merged; calling this method mutates the tensor’s internal representation.- Parameters:
order (
str) – Advanced users seeTensor.value().labels (
Iterable) – The desired subsystem label order, which must be a permutation oflabels. By default, labels are ordered from smallest to biggest.
- Return type:
numpy.ndarray
- apply_matrix(labels, matrix)
Mutates this operator by applying the given square matrix to the given labels.
If acting on \(n\) subsystems, this matrix can be a \(d^n \times d^n\) unitary, or a \(d^{2n}\times d^{2n}\) superoparator. If this operator is currently a unitary and a superoperator is applied,
upgrade()is called. If this state is currently a superoperator and a unitary is applied, the unitary is made into a superoperator before applying.import trueq as tq import numpy as np t = tq.math.OperatorTensor(2) # apply a unitary to qubits 0 and 1 t.apply_matrix((0, 1), tq.Gate.cnot.mat) # apply a 1% bitflip superoperator. this upgrades to a superoperator s = 0.99 * np.eye(4) + 0.01 * np.kron(tq.Gate.x.mat, tq.Gate.x.mat) t.apply_matrix((1,), s) # show the full superoperator tq.plot_mat(t.mat())
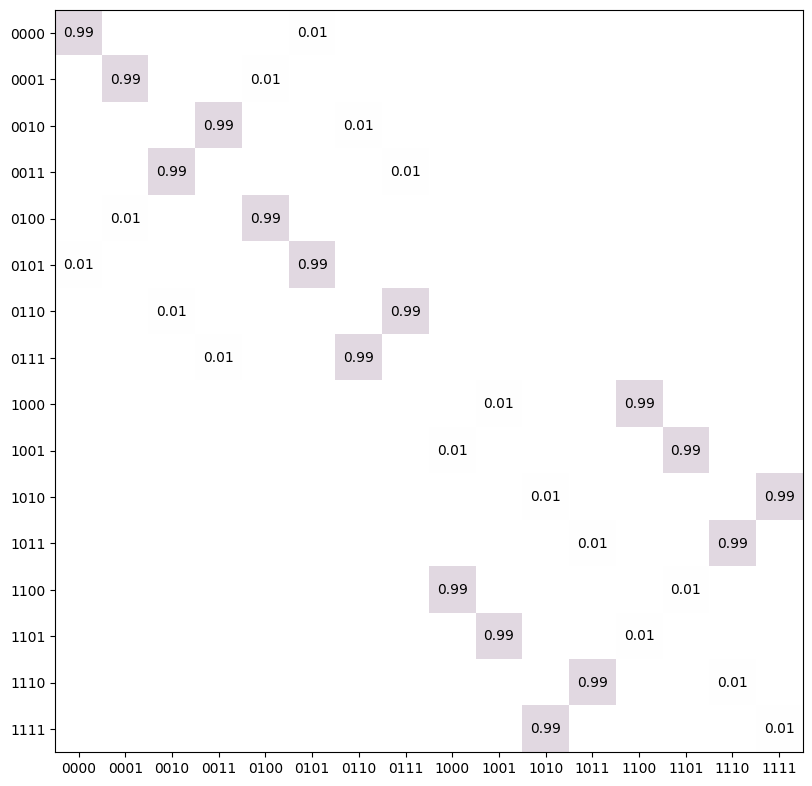
The vectorization convention of superoperators is important. Mixed states are stored in a subsystem-wise row-stacked vectorization convention, and therefore superoperators need to use this convention too. See
to_rowstack_super().- Parameters:
labels (
Iterable) – Which subsystems to apply the matrix to.matrix (
numpy.ndarray-like) – A square matrix.
- diagonal(mat=None, force_real=True)
Returns a new 1D
Tensorwhose values are the diagonal elements of this operator conjugated by the given matrix.For example, if the matrix is the change of basis matrix from the vectorized Pauli basis to the row-stacking basis, then the result is proportional to the Pauli transfer matrix diagonal:
import trueq as tq circuit = tq.Circuit([{(0, 1): tq.Gate.cnot}]) s = tq.Simulator().add_depolarizing(0.01).operator(circuit) # the PTM off by a scale of 2 on every subsystem basis = [tq.math.Weyls(pauli).herm_mat.ravel() for pauli in "IXYZ"] s.diagonal(np.array(basis).T).mat("f")
array([ 4.00000000e+00, 1.98000000e+00, 1.98000000e+00, 2.22044605e-16, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 3.96000000e+00, 1.96020000e+00, 1.96020000e+00, -1.11022302e-16])- Parameters:
mat (
numpy.ndarray) – A dimension-compatible square matrix to change the basis by.force_real (
bool) – Forces thedtypeof the returned tensor to be real.
- Return type:
- trueq.math.tensor.to_rowstack_super(A, B, d, n)
Returns the superoperator of the operation \(X\mapsto AXB^T\) in the subsystem-wise row stacking basis.
See https://arxiv.org/abs/1111.6950 Section V for details on subsystem-wise vs. composite stacking vectorization bases (though beware that this reference uses the column stacking convention).
- Parameters:
A – The left-multiplication operator, a square matrix.
B (
numpy.ndarray) – The right-multiplication operator, a matrix with the same shape as A.d (
int) – The subsystem dimension.n (
int) – The number of subsystems.
- Returns:
The superoperator corresponding to conjugating an input by the given matrices.
- Return type:
numpy.ndarray
Weyl Operators
- class trueq.math.weyl.WeylBase(powers, dim=None)
Base class for symplectic representations of collections and mappings of qudit Weyl operators.
Common to all subclasses, and present in this base class, is a matrix of integer powers which represent the desired operator(s). Each row of the
powersmatrix corresponds to a tensor product of single-qudit Weyls, \(W_{x,z}=\otimes_{j=1,\ldots, n} W_{x_j,z_j}\) where \(x,z\in\mathbb{Z}_d^n\) and \(d\geq 2\) is the subsystem dimension. A single-qudit Weyl is the product of a power of the shift operator, \(X=\sum_{i\in\mathbb{Z}_d}|i+1\rangle\langle i|\), and the clock operator, \(Z=\sum_{i\in\mathbb{Z}_d}e^{2\pi i/d}|i\rangle\langle i|\), given as \(W_{x,z}=X^x Z^z\) for \(x,z\in\mathbb{Z}_d\). For \(d=2\), these correspond to the Pauli operators up to a phase for \(Y\).In a given row of the
powersmatrix, the first half of a row, \(x\), stores the shift operator powers, and the second half of a row, \(z\), stores the clock operator powers; each row of thepowersmatrix represents a multi-qudit Weyl operator. Some subclasses of this base class may contain a vector of phases with one phase for each row of the matrix.For convenience, the constructor allows the
powersmatrix to be specified as a string. For \(d=2\), the strings may be upper case Pauli strings, where multiple multi-qubit Paulis are separated by the_character:from trueq.math.weyl.base import WeylBase p = WeylBase("XXYZ_IXYZ") print(p) p.powers
XXYZ_IXYZ
array([[1, 1, 1, 0, 0, 0, 1, 1], [0, 1, 1, 0, 0, 0, 1, 1]], dtype=uint64)For \(d\geq 2\), single-qudit Weyl operators can be entered in the form, e.g.,
W21which represents \(W_{2,1}\). These are concatenated together, and multiple multi-qudit Weyl operators are separate by the_character:from trueq.math.weyl.base import WeylBase p = WeylBase("W20W11W01_W21W00W02", dim=3) print(p) p.powers
W20W11W01_W21W00W02
array([[2, 1, 0, 0, 1, 1], [2, 0, 0, 1, 0, 2]], dtype=uint64)- Parameters:
powers (
array_like|string|WeylBase) – An array of powers or a string representation, both of which are described above. All numbers are taken the modulo of the dimension at construction. Alternatively, this can also be anotherWeylBase(or child class) instance, from which the powers and dimension will be taken.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim(). This value is unused ifpowersis given as anotherWeylBaseinstance.
- Raises:
ValueError – If
powersargument is empty.ValueError – If a string specification is ragged.
ValueError – If a Pauli string is given but \(d\neq 2\).
ValueError – If an array is given with an odd number of columns.
- DTYPE
alias of
uint64
- ROW_CHAR = '_'
The row separation character for string representations.
- WEYL_CHAR = 'W'
The Weyl prefix character for string representations.
- property dim
The dimension of each subsystem.
- Type:
int
- property powers
The array storing the symplectic representation via powers of the shift and clock operators. See also
x(shift powers) andz(clock powers).- Type:
numpy.ndarray
- property n_sys
The number of qudits in each multi-qudit Weyl.
- Type:
int
- classmethod eye(n_sys, dim=None)
Returns an identity instance of this class.
- Parameters:
n_sys (
int) – The number of subsystems.dim (
int|NoneType) – The subsystem dimension.
- Return type:
- classmethod random(n_sys, n_weyls=1, dim=None, include_id=True)
Returns a random instance of this class.
- Parameters:
n_sys (
int) – The number of subsystems.n_weyls (
int) – The number of multi-qudit Weyls.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().include_id (
bool) – Whether to include any identites in the output.
- Return type:
- classmethod from_dict(dic)
Converts a dictionary representation into a Weyl instance, see also
to_dict().- Parameters:
dic (
dict) – The dictionary representation of the Weyls.- Return type:
- to_dict()
Converts this instance into a dictionary representation, see also
from_dict().- Return type:
dict
- class trueq.math.weyl.WeylDecomp(powers, coeffs, dim=None)
Represents the decomposition of a multi-qudit operator in the Weyl operator basis.
Each operator is decomposed into a vector of coefficients that correspond to each of the Weyl operators. See
WeylBasefor information about the storage format of the Weyl operators.import trueq as tq import trueq.math as tqm import numpy as np # construct a Weyl Decomposition with a list of Weyls and vector of coefficients decomp1 = tqm.WeylDecomp("X_Z", [0.5, 3 - 2j]) # assert that the resulting matrix is as expected mat = 0.5 * tq.Gate.x.mat + (3 - 2j) * tq.Gate.z.mat assert np.allclose(decomp1.mat, mat) # alternatively start with the matrix operator and then calculate decomposition decomp2 = tqm.WeylDecomp.from_mat(mat) assert np.allclose(decomp2.powers, tqm.Weyls("X_Z").powers) assert np.allclose(decomp2.coeffs, [0.5, 3 - 2j]) assert decomp1 == decomp2
- Parameters:
powers (
array_like|string|WeylBase) – A powers matrix specification, as described byWeylBase.coeffs (
array_like) – A vector of complex floats corresponding to the coefficients of each Weyl operator specified by powers.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().
- Raises:
ValueError – If either the powers matrix or coeffs vector have an invalid shape.
- property coeffs
Returns the vector of coefficients that corresponds to each Weyl operator for this instance.
- Type:
ndarray
- classmethod eye(n_sys, dim=None)
Returns an identity instance of this class.
- Parameters:
n_sys (
int) – The number of subsystems.dim (
int|NoneType) – The subsystem dimension.
- Return type:
- classmethod from_mat(mat)
Returns a new instance of this class, as generated by the given operator.
- Parameters:
mat (
array_like) – A mulit-qudit operator, in matrix form.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().
- Raises:
ValueError – If mat is not square.
ValueError – If mat size is greater than 50.
ValueError – If mat size is not a power of dim.
- property mat
Returns the matrix representation of the decomposition stored by this instance. Calculates the summation of the product of each Weyl operator and its corresponding coefficient.
- Type:
ndarray
- classmethod random(n_sys, dim=None)
Returns a random instance of this class. All Weyl operators will be used as a basis for
powers, whilecoeffswill be randomly distributed.- Parameters:
n_sys (
int) – The number of subsystems.n_weyls (
int) – The number of multi-qudit Weyls.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().
- Return type:
- property y_shifted_coeffs
When \(d=2\), returns the vector of coefficients that corresponds to each Pauli operator for this instance. Coefficients for operators with \(Y\) parts will have their phases corrected to match the Paulis rather than \(X^x Z^z\).
- Type:
ndarray- Raises:
ValueError – If
dimis not2.
- class trueq.math.weyl.Weyls(powers, dim=None)
Represents a list of multi-qudit projective Weyl operators.
If the dimension is 2, then this is equivalent to a list of multi-qubit Pauli operators. This class inherits the methods of
WeylBase, and also features additional functions such asall()that would not be suitable for all child classes ofWeylBase. SeeWeylBasefor information about the storage format.import trueq.math as tqm # create a list of two three-qubit Paulis, XYZ and ZIY tqm.Weyls("XYZ_ZIY") # create a list of two three-qutrit Weyls tqm.Weyls("W00W02W11_W11W01W20", 3)
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".- Type:
- Weyls
- Dim:
- 3
- Powers:
X0 X1 X2 Z0 Z1 Z2 0 0 0 1 0 2 1 1 1 0 2 1 1 0 Here are examples exploring some of the main feature of this class:
import trueq.math as tqm # two equivalent ways of creating W_{1, 0}, equal to Pauli X assert tqm.Weyls("X") == tqm.Weyls([1, 0]) # two ways of creating W_{0, 1} W_{2, 3} in dimension 5 assert tqm.Weyls("W01W23", 5) == tqm.Weyls([[0, 2, 1, 3]], 5) # two equivalent ways to list all single qubit Weyls, I, X, Y, Z assert tqm.Weyls("I_X_Y_Z") == tqm.Weyls([[0, 0], [1, 0], [1, 1], [0, 1]]) # get the first three qubit Pauli from a list assert tqm.Weyls("XYZ_ZIY")[0, :] == tqm.Weyls("XYZ") # get a list of the Weyl operators acting on only the second qutrit assert tqm.Weyls("W00W02W11_W11W01W20", 3)[:, 1] == tqm.Weyls("W02_W01", 3) # Weyls can be multiplied, up to a phase assert tqm.Weyls("X") @ tqm.Weyls("Y") == tqm.Weyls("Z") # mutliplication distributes across broadcastable shapes assert tqm.Weyls("X") @ tqm.Weyls("X_Y_Z_I") == tqm.Weyls("I_Z_Y_X")
- Parameters:
powers (
array_like|string|WeylBase) – A powers matrix specification, as described byWeylBase.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim(). This value is unused ifpowersis given as anotherWeylBaseinstance.
- property iter_sys
An iterator yielding each subsystem of this instance as a new single-qudit
Weyls.- Type:
generator
- property n_weyls
The number of multi-qudit Weyls stored in this instance.
- Type:
int
- property gate
Constructs and returns the unitary matrix representation of this Weyl operator in the canonical basis as a
Gate. If this instance contains multiple Weyl operators, that is, ifn_weylsis greater than 1, an error will be raised. In this case, considergatesinstead.For example,
import trueq as tq import trueq.math as tqm assert tqm.Weyls("XX").gate == tq.Gate.x & tq.Gate.x # note that there is a -I phase difference here which Gate equality ignores assert tqm.Weyls("Y").gate == tq.Gate.y
- Type:
- Raises:
ValueError – If this instance contains more than one multi-qudit Weyl.
- property gates
Constructs and returns a list containing the unitary matrix representations of each Weyl operator in this instance, in the canonical basis as a
Gate.For example,
import trueq as tq import trueq.math as tqm assert tqm.Weyls("Y").gates == [tq.Gate.y] assert tqm.Weyls("XX").gates == [tq.Gate.x & tq.Gate.x] assert tqm.Weyls("I_Z").gates == [tq.Gate.id, tq.Gate.z]
- Type:
list
- property herm_mat
A Hermitian version of
matsuch that:Each distinct multi-qudit Weyl operator results in a fixed, unique Hermitian matrix.
Matrices on \(n\) \(d\)-dimensional subsystems are normalized to \(\sqrt{d^n}\).
Unequal multi-qudit Weyl operators result in orthogonal matrices.
When \(d=2\) the usual multi-qubit Pauli matrices are used, where, in particular, \(Y=\left(\begin{smallmatrix}0&-i\\i&0\end{smallmatrix}\right)\) rather than \(XZ=iY\), as used by
mat.The span of any set of multi-qudit Weyl operators along with their adjoints results in the corresponding span of these Hermitian matrices.
The above properties are obtained with the following construction, where, unlike other methods and attributes of this class, we use the phase convention \(W_{x,z}=e^{i \pi xz}X^xZ^z\) for a pair of powers \(x,z\in\mathbb{Z}_d\). This is done to ensure the orthogonality criterion. Given some \(W_{x,z}\), its adjoint is \(W_{x,z}^\dagger=W_{-x,-z}=e^{i \pi xz}X^{-x}Z^{-z}\), and a Hermitian matrix is constructed from it by normalizing either \(W_{x,z}+W_{x,z}^\dagger\) or \(iW_{x,z}-iW_{x,z}^\dagger\). The former choice is made whenever \((x,z)>=(d-x,d-z)\mathrm{mod}d\) lexicographically, and the latter choice is made otherwise.
Like
mat, the return shape is 3D ifn_weylsis greater than one, where the output’s first index is over multi-qudit Weyls, otherwise the return shape is 2D.- Type:
ndarray
- property mat
The matrix representation, or an array of matrix representations, of the Weyl(s) contained in this instance, in the canonical basis. The return shape is 3D if
n_weylsis greater than one where the first index is over multi-qudit Weyls, otherwise the return shape is 2D.- Type:
ndarray
- classmethod all(n_sys, dim=None, include_id=True, lex=True)
Returns a new
Weylsinstance where every possible projective multi-qudit Weyl operator appears as a row.If
lexisTrue, then the order is primarily lexicographic in the subsystems with the right-most subsystem rastering fastest, and secondarily lexicographic in the integer pair(x, z)for each subsystem. Otherwise, the secondary ordering is chosen so that operators that are adjoints of each other are adjacent, and also so that when \(d=2\), the subsystem order is \(I, X, Y, Z\).- Parameters:
n_sys (
int) – The number of subsystems.dim (
int|NoneType) – The subsystem dimension.include_id (
bool) – Whether to include any identites in the output.lex (
bool) – Whether to order subsystems lexicographically in \((x,z)\), as described above.
- Return type:
- delete_duplicates(herm_equal=False)
Returns a new instance where the rows have been sliced to only contain Weyls which are not equal to each other. Optionally, two rows can be treated as equal when they are adjoints of each other. The returned instance will have rows sorted in the same way that
all()sorts rows whenlex=False.import trueq.math as tqm # remove duplicate rows assert tqm.Weyls("XX_YY_XY_XX").delete_duplicates() == tqm.Weyls("XX_XY_YY") # remove duplicate rows, including adjoints weyl1 = tqm.Weyls("W11_W12_W22", dim=3) weyl2 = tqm.Weyls("W11_W12", dim=3) assert weyl1.delete_duplicates(True) == weyl2
- Parameters:
herm_equal (
bool) – Whether or not to treat rows which are equal to each other up to an adjoint as equal. In such a case, the row with the lowerindices()(withlex=False) is kept. This flag is not relevant for qubit systems because no distinct Paulis are adjoints of each other.- Return type:
- class trueq.math.weyl.WeylSet(powers, dim=None)
Represents a set of multi-qudit projective Weyl operators.
If the dimension is 2, then this is equivalent to a set of multi-qubit Pauli operators. See
WeylBasefor information about the storage format.The only difference between this class and its parent,
Weyls, is that this class automatically sorts and deletes duplicate rows of the given powers matrix during construction.import trueq.math as tqm # create a set of three-qubit Paulis, and note that the duplicate row is removed # and that the remaining rows are sorted. tqm.Weyls("XYZ_XYZ_ZIY_XYZ")
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".- Type:
- Weyls
- Dim:
- 2
- Powers:
X0 X1 X2 Z0 Z1 Z2 0 1 1 0 0 1 1 1 1 1 0 0 1 1 2 0 0 1 1 0 1 3 1 1 0 0 1 1 - Parameters:
powers (
array_like|string|WeylBase) – A powers matrix specification, as described byWeylBase.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim(). This value is unused ifpowersis given as anotherWeylBaseinstance.
- classmethod all(n_sys, dim=None, include_id=True)
Returns a new
Weylsinstance where every possible projective multi-qudit Weyl operator appears as a row.- Parameters:
n_sys (
int) – The number of subsystems.dim (
int|NoneType) – The subsystem dimension.include_id (
bool) – Whether to include any identites in the output.
- Return type:
- class trueq.math.weyl.Stabilizers(powers, phase_ints, dim=None)
Class that represents a list of multi-qudit Weyl operators with associated phases that are constrained to certain discrete values on the unit circle.
Specifically, each multi-qudit Weyl operator in an instance of this class must leave a nontrivial subspace invariant and so cannot generate a group that contains nontrivial multiples of the identity. Common parent class to
CliffordandStabilizerGroup.An instance of this class contains a representation in terms of two integer arrays. The first is an array of powers, where the left half contains powers of the single-qudit \(X\) operator, and the right half contains powers of the single-qudit \(Z\) operator, so that each row represents a multi-qudit operator. The second is a vector of phase powers, one for each multi-qudit operator. For a particular multi-qudit operator with length-\(n\) power vectors \(x\) and \(z\), a phase integer of value \(j\) results in a phase of \(exp(\pi i (2j + (x.z \% 2)) / d)\) for \(d=2\), and a phase of \(exp(2\pi ij/ d)\) for \(d>2\).
import trueq.math as tqm # define stabilizers using two Weyls and a list of phases stab_pauli = tqm.Stabilizers(tqm.Weyls("W00W11_W00W22"), [0, 1]) # get the list of phases in complex form stab_pauli.phases
array([ 6.123234e-17+1.0000000e+00j, -1.000000e+00+1.2246468e-16j])
- Parameters:
powers (
array_like|string|WeylBase) – A powers matrix specification, as described byWeylBase.phase_ints (
array_like) – A vector of integers corresponding to the phases of each Weyl operator specified by powers.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().
- Raises:
ValueError – If either the powers matrix or phase_ints vector have an invalid shape.
- property phase_ints
The array corresponding to the phases of each Weyl generator in the stabilizer group, represented as integers modulo
dim.- Type:
numpy.ndarray
- property phases
The array corresponding to the phases of each Weyl generator in the stabilizer group, evaluated to their complex values.
- Type:
numpy.ndarray
- apply(clifford, subsystems=None)
Returns a new
Stabilizersobject with the same type asselfwhere (a subset of subsystems of) rows have been taken to their image under theCliffordoperation.When
selfis also a Clifford operation, this results in standard Clifford multiplication, wheresubsystemsprovides the option to multiply a small Clifford into selected subsystems of some larger Clifford.import trueq.math as tqm cx = tqm.Clifford.cx() # apply a random single-qubit Clifford onto the second half of a CX cx.apply(tqm.Clifford.random(1), [1])
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".- Type:
- Clifford
- Dim:
- 2
- Generator images:
X0 X1 Z0 Z1 ph. im(X0) 1 0 0 1 1 im(X1) 0 0 0 1 1 im(Z0) 0 0 1 0 0 im(Z1) 0 1 1 1 1 Note
When
subsystems=None, the Clifford is applied to all subsystems of this object, so that this method becomes identical toother @ self. Notice, in particular, thatothercomes beforeself(in contrast toself.apply(other)) because@has been implemented to conform to the standard matrix multiplication ordering.- Parameters:
- Return type:
- classmethod eye(n_sys, dim=None)
Returns an identity instance of this class.
- Parameters:
n_sys (
int) – The number of subsystems.dim (
int|NoneType) – The subsystem dimension.
- Return type:
- classmethod random(n_sys, n_weyls=1, dim=None)
Returns a random instance of this class.
- Parameters:
n_sys (
int) – The number of subsystems.n_weyls (
int) – The number of multi-qudit Weyls.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().
- Return type:
- class trueq.math.weyl.Clifford(powers, phase_ints, dim=None)
Represents a multi-qudit Clifford operator via its symplectic representation.
See
WeylBaseandStabilizersfor more information.An \(n\)-qudit Clifford is fully defined by its action on a set of generators of the Weyl group on \(n\)-qudits. For consistency, we fix this set of generators to be the Weyl \(X\) and \(Z\) Weyl operators on each qudit. These generators are ordered as \(X_1\) through \(X_n\) followed by \(Z_1\) through \(Z_n\), where \(n\) is the number of qudits in the system.
Below is an example in which we define a two-qubit Clifford that maps \(XI \rightarrow IX, IX \rightarrow XI, ZI \rightarrow IZ, IZ \rightarrow ZI\), and a single-qutrit Clifford which maps \(X \rightarrow Z, Z\rightarrow X\).
import trueq as tq import trueq.math as tqm import numpy as np # define a set of 4 two-qubit Paulis paulis = tqm.Weyls("IX_XI_IZ_ZI") # define a Clifford with the generating set mapping to the above ordered Paulis cliff = tqm.Clifford(paulis, [0, 0, 0, 0]) IX = tq.Gate.id & tq.Gate.x XI = tq.Gate.x & tq.Gate.id assert np.array_equal(cliff.mat @ IX @ cliff.mat.conj(), XI)
We can also perform standard operations on Clifford operators:
import trueq.math as tqm # create a random 3 qubit Clifford, and a random 2 qubit Clifford a = tqm.Clifford.random(3) b = tqm.Clifford.random(2) # kronecker them together, and multiply against another random 5 qubit Clifford d = (a & b) @ tqm.Clifford.random(5) print(d) # multiply a 2 qubit CX into positions 4 and 2 of our 5 qubit Clifford e = d.apply(tqm.Clifford.cx(), [4, 2]) print(e)
Clifford('ZYXYZ_ZIZIY_YYXIY_IYYIX_XIYII_IYIXI_YZZZI_IXIYY_XIIXZ_XZZYX', [1, 0, 0, 1, 0, 1, 0, 1, 0, 1]) Clifford('ZYXYZ_ZIYIX_YYIIY_IYZIY_XIYIZ_IYIXI_YZZZZ_IXXYY_XIIXZ_XZYYY', [1, 0, 0, 1, 0, 1, 0, 1, 0, 1])- Parameters:
powers (
array_like|string|WeylBase) – A powers matrix specification, as described byWeylBase. Any provided input will be turned into a sorted list of generators which produce the same stabilizer group.phase_ints (
array_like) – A vector of integers corresponding to the phases of each Weyl operator specified by powers.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().
- Raises:
ValueError – If either the powers matrix or phase_ints vector have an invalid shape.
ValueError – If this Clifford does not preserve commutation relations
- static random(n_sys, dim=None)
Construct a random Clifford on
n_sysqudit subsystems of dimensiondim.- Parameters:
n_sys (
int) – The number of subsystems.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().
- Return type:
- property mat
Returns the unitary representation of a Clifford operation.
- Type:
ndarray
- static eye(n_sys, dim=None)
Returns an identity instance of this class.
- Parameters:
n_sys (
int) – The number of subsystems.dim (
int|NoneType) – The subsystem dimension.
- Return type:
- static fourier(dim=None)
Returns a Fourier
Cliffordgate acting on a qudit of dimensiondim, as defined in [18]. The FourierCliffordgate maps \(X \rightarrow Z, Z \rightarrow X^{-1}\), and can thus be regarded as a generalization of the Hadamard gate to qudits.- Parameters:
dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().- Return type:
- static cz(dim=None)
Returns a generalized CZ
Cliffordgate acting on two qudits of dimensiondim, as defined in [18].- Parameters:
dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().- Return type:
- static cx(dim=None)
Returns a generalized CX
Cliffordgate acting on two qudits of dimensiondim, as defined in [18].- Parameters:
dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().- Return type:
- static swap(perm=(1, 0), dim=None, invert_perm=False)
Returns a
Cliffordwhich swaps subsytems as specified by a permutation vector.import trueq.math as tqm # create a clifford that shifts subsystems to the left cyclically tqm.Clifford.swap([2, 0, 1])
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".- Type:
- Clifford
- Dim:
- 2
- Generator images:
X0 X1 X2 Z0 Z1 Z2 ph. im(X0) 0 0 1 0 0 0 0 im(X1) 1 0 0 0 0 0 0 im(X2) 0 1 0 0 0 0 0 im(Z0) 0 0 0 0 0 1 0 im(Z1) 0 0 0 1 0 0 0 im(Z2) 0 0 0 0 1 0 0 - Parameters:
perm (
Iterable) – An iterable whose length is the total number of subsystems,n_sys, and that contains every integer0, 1, ..., n_sys-1exactly once. The default value,(1, 0), results in the usual two-system SWAP gate.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().invert_perm (
bool) – Whether to invert the provided permutation vectorperm.
- Return type:
- class trueq.math.weyl.StabilizerGroup(powers, phase_ints, dim=None)
A class which stores the symplectic representation of an Abelian group of multi-qudit stabilizer operators.
See
WeylBaseandStabilizersfor more information.For a given set of generators, this class will automatically check if the set is reducible and find a minimal set of generators for the group. Once constructed, class property state can be used to obtain a pure state that is invariant under all elements of this group.
import trueq.math as tqm import numpy as np # define a stabilizer group using two two-qudit Paulis and a list of phases weyl = tqm.Weyls("YI_IY") stab = tqm.StabilizerGroup(weyl, [0, 1]) # observe that the pure state is invariant under the elements in this group state = stab.state assert np.allclose((stab.phases[0] * weyl.gates[0]) @ state, state) assert np.allclose((stab.phases[1] * weyl.gates[1]) @ state, state)
- Parameters:
powers (
array_like|string|WeylBase) – A powers matrix specification, as described byWeylBase. Any provided input will be turned into a sorted list of generators which produce the same stabilizer group.phase_ints (
array_like) – A vector of integers corresponding to the phases of each Weyl operator specified by powers.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().
- Raises:
ValueError – If either the powers matrix or phase_ints vector have an invalid shape.
ValueError – If some of the elements of the group do not commute.
- classmethod random(n_sys, k=0, dim=None)
Construct a random stabilizer group over
n_sysqudit subsystems of dimensiondim. This stabilizer group will act onklogical qudits and thus will haven_sysminuskWeyl generators.- Parameters:
n_sys (
int) – The number of subsystems.k (
int) – The number of logical qudits. The default value of0will result in a pure state specified byn_sysgenerators.dim (
int|NoneType) – The qudit dimension, which must be one ofSMALL_PRIMES. The default value ofNonewill result in the default dimension obtained fromget_dim().
- Return type:
- property state
Returns a pure state in the simultaneous
+1eigenspace of all elements in the stabilizer group.- Return type:
ndarray
