Cycle

class trueq.Cycle(content=None, marker=0, dim=None)

Represents a “clock cycle” of a Circuit; a set of Gates that happen in parallel to a disjoint set of systems. The storage format is a dict that maps tuples of system labels to Gate objects. Any given system can only be addressed once in a Cycle.

This class is iterable, yielding tuples of the form (labels, gate).

import trueq as tq

# Single system operations can be applied to multiple systems at once
cycle = tq.Cycle({(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t})

for labels, operation in cycle:
    print(f"Labels: {str(labels): <8}\tOperation: {operation}")

Labels: (0, 1)  	Operation: Gate.cx
Labels: (2,)    	Operation: Gate.t
Labels: (3,)    	Operation: Gate.t
Labels: (4,)    	Operation: Gate.t

Compilation tools will only perform actions on lists of contiguous cycles with equal markers; markers serve as a compiler directive describing which portions of a circuit can be recompiled as a block.

Parameters:

content (dict) – A dict whose keys are tuples and whose values are Operations; the method add() is called on each pair.
marker (int) – An identifier used to label related cycles for compiler and benchmarking tools.
dim (int | NoneType) – The dimension of each subsystem that gates in this cycle act on, which must be consistent with all provided content. If None, which is default, then the dimension is inferred by any provided Gates, and if none are present, then the value is set to the value of get_dim().

property dim

The dimension of each subsystem, e.g. 2 if this cycle acts on qubits.

import trueq as tq

cycle = tq.Cycle({(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t})
cycle.dim

Type:: int

property labels

The sorted union of all system labels acted on by Operations in this Cycle.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.labels

(0, 1, 2, 3, 4, 5, 6)

Type:: tuple

property n_gates

The number of gates in this Cycle.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.n_gates

Type:: int

property n_meas

The number of measurements (Meas) in this Cycle.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.n_meas

Type:: int

property n_prep

The number of preparations (Prep) in this Cycle.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.n_prep

Type:: int

property n_operations

The total number of operations in this Cycle, equal to the sum of n_gates, n_meas, and n_prep.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.n_operations

Type:: int

property n_sys

The number of distinct systems participating in this Cycle.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.n_sys

Type:: int

property gates

The dict of Gates in this Cycle.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.gates

{(0, 1): Gate.cx, (2,): Gate.t, (3,): Gate.t, (4,): Gate.t}

Type:: dict

property gates_single

The single-qubit gates of this cycle; a dict of Gates in this Cycle that act on one subsystem.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.gates_single

{(2,): Gate.t, (3,): Gate.t, (4,): Gate.t}

Type:: dict

property gates_multi

The multi-qubit gates of this cycle; a dict of Gates in this Cycle that act on at least two subsystems.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.gates_multi

{(0, 1): Gate.cx}

Type:: dict

property gate_labels

A sorted tuple of all labels in the cycle that have gates (i.e. labels that point to a Gate operation).

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.gate_labels

(0, 1, 2, 3, 4)

Type:: tuple

property prep

The dict of Preps in this Cycle.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.prep

{(6,): Prep()}

Type:: dict

property prep_labels

A sorted tuple of all labels in the cycle that are a preparation (i.e. labels that point to a Prep operation).

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.prep_labels

(6,)

Type:: tuple

property meas

The dict of Meass in this Cycle.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.meas

{(5,): Meas()}

Type:: dict

property meas_labels

A sorted tuple of all labels in the cycle that are a preparation (i.e. labels that point to a Meas operation).

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.meas_labels

(5,)

Type:: tuple

property operations

The total dict of Operations in this Cycle.

import trueq as tq

cycle = tq.Cycle(
    {(0, 1): tq.Gate.cnot, (2, 3, 4): tq.Gate.t, 5: tq.Meas(), 6: tq.Prep()}
)
cycle.operations

{(0, 1): Gate.cx,
 (2,): Gate.t,
 (3,): Gate.t,
 (4,): Gate.t,
 (6,): Prep(),
 (5,): Meas()}

Type:: dict

contained_gates(labels)

Yields the pairs of labels and gates of this Cycle on the given labels. If the label only contains a partial overlap with a Gate in this Cycle, it will not be included.

import trueq as tq

cycle = tq.Cycle({0: tq.Gate.x, (1, 2): tq.Gate.cx, 3: tq.Gate.x})
{labels: gate for labels, gate in cycle.contained_gates([0, 3])}

{(0,): Gate.x, (3,): Gate.x}

Parameters:: labels (Iterable) – A labels to restrict this cycle to.
Return type:: generator

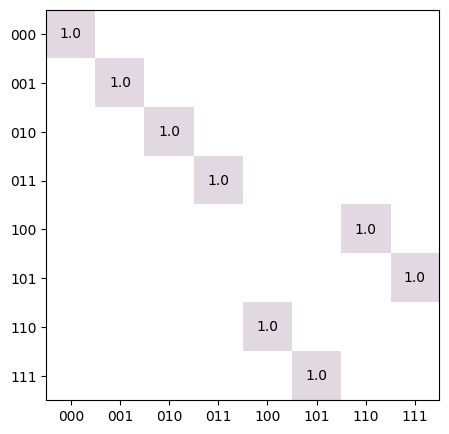
tensor(labels=None)

Returns a Tensor representation of the Gates in this Cycle.

The matrix representation (which will be exponentially sized in the number of systems!) of this cycle can be obtained with:

import trueq as tq

cycle = tq.Cycle({(0, 1): tq.Gate.cx, 2: tq.Gate.i})
matrix = cycle.tensor().mat()
tq.plot_mat(matrix)

Parameters:: labels (list) – An optional list of labels to force into the tensor in case they are not already present as labels in this cycle.
Return type:: Tensor

is_equivalent(other, ignore_marker=True, ignore_id=True)

Checks if this cycle is equivalent to another cycle.

import trueq as tq

cycle1 = tq.Cycle({(0, 1): tq.Gate.cx})
cycle2 = tq.Cycle({(0, 1): tq.Gate.cx})
cycle1.is_equivalent(cycle2)

True

Parameters:

other (Cycle) – Another cycle to compare this one to.
ignore_marker (bool) – Whether to ignore the marker values. Default is True.
ignore_id (bool) – Whether to treat all identity gates as though they are not present. Default is True.

Return type:

bool

same_structure(other)

Determine if this cycle has the same structure as the other cycle, that is if it is identical to another cycle except for the parameters of any NativeGates. See also same_structure().

For a rudimentary example, see below. For a detailed example using gate factories and the compiler, see same_structure().

import trueq as tq

# the following cycles are defined so that they have the same structure
nx = tq.NativeGate.from_generators("rx", "X", 180, params={"theta": 180})
nx1 = tq.NativeGate.from_generators("rx", "X", 90, params={"theta": 90})
cycle1 = tq.Cycle({0: tq.Meas(), 1: nx, 2: tq.Gate.z})
cycle2 = tq.Cycle({0: tq.Meas(), 1: nx1, 2: tq.Gate.z})

# as stated, these cycles have the same structure, but are not equal
assert cycle1 != cycle2
assert cycle1.same_structure(cycle2)

Parameters:: other (Cycle) – Another cycle to compare to.
Return type:: bool

to_dict()

Returns a dictionary representation of a Cycle object. This dictionary representation contains only base Python classes.

import trueq as tq

cycle = tq.Cycle({(0, 1): tq.Gate.cx})
cycle.to_dict()

{'content': {(0, 1): ('Gate',
   {'u': (((1+0j), 0j, 0j, 0j),
     (0j, (1+0j), 0j, 0j),
     (0j, 0j, 0j, (1+0j)),
     (0j, 0j, (1+0j), 0j))})},
 'marker': 0,
 'dim': 2}

Return type:: dict

static from_dict(dic)

Returns a Cycle constructed from a dictionary representation.

import trueq as tq

cycle = tq.Cycle({(0, 1): tq.Gate.cx})
cycle.from_dict(cycle.to_dict())

True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".

(0, 1): Gate.cx

Parameters:: dic (dict) – A dictionary used to construct a new Cycle.
Return type:: Cycle

property marker

An identifier used to label related cycles for compiler and benchmarking tools.

This defaults to 0 but can be optionally set to any positive int.

Type:: int