Simulation
A (noisy) quantum simulator for |
|
A noise source which inserts or replaces entire cycles during simulation. |
|
Appends a noise source to this simulator that adds isotropic depolarizing noise to the simulation. |
|
Adds a noise source that replaces all matched |
|
A noise source which emulates the noise measured in a KNR experiment. |
|
Appends a noise source to this simulator that adds Kraus noise to the simulation. |
|
Appends a noise source to this simulator that performs gate over/underrotation. |
|
Appends a state preparation description to this simulator that chooses which state to prepare whenever a preparation instruction is encountered in a circuit. |
|
Appends measurement classification error to this simulator, where errors are specified by confusion matrices estimated by the readout calibration protocol (RCAL). |
|
Appends measurement classification error and/or positive operator valued measurement (POVM) error to this simulator. |
|
Appends a noise source to this simulator that adds \(T_1\) and \(T_2\) relaxation noise to the simulation. |
|
Appends a noise source to this simulator that introduces stochastic Pauli noise. |
|
Computes the dressed noise of the given cycle. |
|
Returns the unitary or superoperator that results from simulating the given circuit. |
|
Predicts the estimates that would be generated by simulating |
|
Predicts the estimates that would be generated by simulating |
|
Predicts the estimates that would be generated by simulating |
|
Predicts the estimates that would be generated by simulating |
|
Updates the |
|
Returns the quantum state that results from simulating the given |
|
Abstract parent class for all simulation backends. |
|
Measurement policies for simulation backends. |
|
Preparation policies for simulation backends. |
|
A simulation backend that uses |
|
Parent class for all built in noise sources which can be added to the simulator. |
|
A class whose purpose is to filter the operations presented to a given |
|
Wraps a |
|
Wraps labels and an |
Simulator
- class trueq.Simulator(backend=None)
A (noisy) quantum simulator for
Circuitobjects that can be used to compute the finalstate(), the total effectiveoperator(), or simplyrun()them tosample()shots.import trueq as tq # initialize a simulator with no noise present sim = tq.Simulator() # initialize a simulator with depolarizing noise at rate 1% sim = tq.Simulator().add_depolarizing(0.01) # initialize a simulator with depolarizing noise at rate 1%, and unitary # overration by 5% sim = tq.Simulator().add_depolarizing(0.01).add_overrotation(0.05) # make some circuits and populate their results with random shots circuits = tq.make_srb([0], [4, 60]) sim.run(circuits, n_shots=100) circuits[0].results
Results({'0': 97, '1': 3})- Parameters:
backend (
SimulationBackend) – A backend to perform simulations with.
- property backend
The backend of this simulator instance.
- Type:
- get_dim(circuit)
Returns the subsystem dimension this simulator would use for the given circuit. This dimension is determined by first checking whether any of the
noise_sourcesdemand a specific dimension, returning it if a consistent one is found. Otherwise, the subsystem dimension of the given circuit is used. In the edge case that the circuit is empty and no noise source specifies a dimension,trueq.settings.get_dim()is used.- Parameters:
circuit (
Circuit) – A circuit to be simulated.- Return type:
py:class:int
- property noise_sources
The noise sources that have been added to this simulator. They are ordered in the same way that they are applied to any given cycle.
An instance of the noiseless simulator
NoiseSourcealways appears at the end, which handles the simulation of any gates which other noise sources ignored.- Type:
list
- append_noise_source(noise_source)
Appends a noise source to the simulator. A noise source in an instance of some subclass of
NoiseSource, which includes custom user subclasses.The order in which noise sources are added is the order in which they will be applied (cycle by cycle) during simulation.
- Parameters:
noise_source (
NoiseSource) – A source of noise to be added to the simulator.- Returns:
This simulator instance.
- Return type:
- Raises:
ValueError – If the dimension of the noise source conflicts with an existing dimension.
- process(circuit, prep_policy, meas_policy, n_shots=None)
A low-level interface to this simulator where backend policies can be specified manually. See
operator(),state(),sample(), andrun()for wrappers of this function that specify the policies automatically and invoke the final type.This method loops over cycles of the given circuit, and for each one loops over noise sources, which are in turn given the oportunity to call methods of the backend such as
process_gate(). This method does not necessarily perform the quantum simulation as some backends may elect to use the processing time to introspect and store the instructions rather than simulate them. Seevalue.- Parameters:
circuit (
Circuit|Cycle|dictIterable) – A circuit to simulate. This can also be any valid first argument to theCircuitconstructor, such as aCycle,dict, or iterable of these two.prep_policy (
PrepPolicy) – A policy specifying how to process preparation instructions.meas_policy (
MeasPolicy) – A policy specifying how to process measurement instructions.n_shots (
None|int|inf) – If relevant, the number of shots to sample from measurements of the circuit. This can be a positive integer, or something equal tofloat("inf")to report the probability of every outcome.
- Return type:
- operator(circuit)
Returns the unitary or superoperator that results from simulating the given circuit.
If this simulator contains only unitary errors and pure state preparations, a unitary will be simulated and returned, otherwise, a superoperator will be simulated and returned.
import trueq as tq # make a circuit with two clock cycles circuit = tq.Circuit([{(0,): tq.Gate.h}, {(0, 1): tq.Gate.cnot}]) # simulate the circuit to find the final unitary u = tq.Simulator().operator(circuit) tq.plot_mat(u.mat()) # if we add depolarizing noise we get a superoperator s = tq.Simulator().add_depolarizing(0.01).operator(circuit) print("Super operator shape: ", s.mat().shape)
Super operator shape: (16, 16)
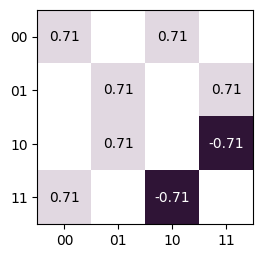
- Parameters:
circuit (
Circuit) – A circuit to find the final operator of.- Returns:
The effective operator of the circuit after simulation.
- Return type:
- Raises:
NotImplementedError – If the last cycle in the circuit contains measurements on some qubits but not all.
- run(circuits, n_shots=50, overwrite=None, max_workers=1)
Updates the
resultsattribute of each given circuit by simulating its final quantum state and sampling shots from it.import trueq as tq # make a circuit with two clock cycles and a measurement round circuit = tq.Circuit([{(0,): tq.Gate.h}, {(0, 1): tq.Gate.cnot}]) circuit.measure_all() # initialize a simulator with no noise sim = tq.Simulator() # run the circuit on the simulator 100 times to populate the results sim.run(circuit, n_shots=100) print(circuit.results) # instantiate a simulator with depolarizing and overrotation noise sim = tq.Simulator().add_depolarizing(0.01).add_overrotation(0.04) # we can also use run to evaluate circuit collections generated by protocols # like CB, SRB, IRB, and XRB on a simulator: circuits = tq.make_srb([0], [5, 50, 100], 30) sim.run(circuits, n_shots=100) circuits.plot.raw()
Results({'00': 47, '11': 53})
- Parameters:
circuits (
Circuit|Iterable) – A single circuit or an iterable of circuits.n_shots (
int|float("inf")) – The number of shots to sample. The final state of the circuit is simulated once and shots are drawn from the resulting probability distribution. Or, if this value is infinity-like (e.g.float("inf")ornumpy.inf) then results are populated with the exact simulated probabilities.overwrite (
bool|NoneType) – IfFalse, a circuit that already has results will have new simulation results added to the old results. IfTrueorNone, old results will be erased and replaced with new results, though a warning will be raised in the latter case ofNone(default).max_workers (
int|NoneType) – The maximum number of workers to use when parallelizing this simulation over circuits. A value ofNonedefaults to the number of processors on the machine. This feature is not available on Windows, which defaults to serial simulation.
- sample(circuit, n_shots=50)
Samples ditstrings from the final state of the simulated circuit. In contrast to
run(), this method does not update the results of the circuit.import trueq as tq # make a circuit with two clock cycles and a measurement round circuit = tq.Circuit([{(0,): tq.Gate.h}, {(0, 1): tq.Gate.cnot}]) circuit.measure_all() # instantiate a simulator with depolarizing and overrotation noise sim = tq.Simulator().add_depolarizing(0.01).add_overrotation(0.04) # sample 100 shots from the final state of the circuit print(sim.sample(circuit, 100))
Results({'00': 48, '11': 52})- Parameters:
circuit (
Circuit) – A single circuit.n_shots (
int|float("inf")) – The number of shots to sample. The final state of the circuit is simulated once and shots are drawn from the resulting probability distribution. Or, if this value is infinity-like (e.g.float("inf")ornumpy.inf) then results are populated with the exact simulated probabilities.
- Return type:
- state(circuit)
Returns the quantum state that results from simulating the given
circuit.If this simulator contains only unitary errors and pure state preparations, a pure state will be simulated and returned, otherwise, a density matrix will be simulated and returned. Unless this simulator contains a special preparation (see e.g.
add_prep()), every qubit in the circuit will be prepared with the state \(|0\rangle\).import trueq as tq # make a circuit with two clock cycles circuit = tq.Circuit([{(0,): tq.Gate.h}, {(0, 1): tq.Gate.cnot}]) # simulate the circuit to find the final pure state psi = tq.Simulator().state(circuit) print("Pure state: ", psi.mat()) # if we add depolarizing noise we get a density matrix rho = tq.Simulator().add_depolarizing(0.01).state(circuit) print("Density matrix: ", rho.mat()) # we can get outcome probabilities from the state print("Pure state probabilities: ", psi.probabilities()) print("Density matrix probabilities: ", rho.probabilities()) # and we can convert them to Result objects print("Pure state as results: ", psi.probabilities().to_results()) print("Density matrix as results: ", rho.probabilities().to_results())
Pure state: [0.70710678+0.j 0. +0.j 0. +0.j 0.70710678+0.j] Density matrix: [[0.4975 +0.j 0. +0.j 0. +0.j 0.48759975+0.j] [0. +0.j 0.0025 +0.j 0.00245025+0.j 0. +0.j] [0. +0.j 0.00245025+0.j 0.0025 +0.j 0. +0.j] [0.48759975+0.j 0. +0.j 0. +0.j 0.4975 +0.j]] Pure state probabilities: Tensor(<[(2,), ()] on labels [(0, 1)]>) Density matrix probabilities: Tensor(<[(2,), ()] on labels [(0, 1)]>) Pure state as results: Results({'00': 0.5000000000000001, '11': 0.5000000000000001}) Density matrix as results: Results({'00': 0.4975000000000001, '01': 0.0025000000000000005, '10': 0.0025000000000000005, '11': 0.4975000000000001})- Parameters:
circuit (
Circuit) – A circuit to find the final state of.- Return type:
- Raises:
NotImplementedError – If the circuit contains measurements before the final cycle.
- add_cycle_noise(replacement, match, cycle_offset=0, dim=None)
A noise source which inserts or replaces entire cycles during simulation. The
replacementcycle can be specified as a cycle-like object, or a function which takes in a cycle and returns a cycle-like. A cycle-like is either a cycle or a dictionary mapping labels to operations. The operations contained in this dictionary can beGates and /orSuperops.The relative location of cycle insertion or replacement is determined by
cycle_offset; a value of-1inserts the noisy cycle before the matched cycle,0inserts the cycle in place of the matched cycle, and+1inserts the cycle after the matched cycle. These are the only allowed values. The match owned by this instance must be a child class ofBaseCycleMatch. This restriction allows the noise source to match on past cycles and thus has the ability to simulate non-Markovian noise.Some examples are provided below:
import trueq as tq import trueq.math as tqm import trueq.simulation as tqs import numpy as np cyc_h = tq.Cycle({0: tq.Gate.h, 3: tq.Gate.h}) cyc_cx = tq.Cycle({(0, 1): tq.Gate.cx}) cyc_cz = tq.Cycle({(0, 1): tq.Gate.cz}) m_h = tqs.CycleMatch(cyc_h, lag=1) m_cx = tqs.CycleMatch(cyc_cx) m_cz = tqs.CycleMatch(cyc_cz) # insert a small flip angle cycle before any CNOT cycles circuit1 = tq.Circuit([cyc_h, cyc_cx]) small_flip = {(0, 1): tq.Gate.rx(10)} sim1 = tq.Simulator() sim1.add_cycle_noise(small_flip, cycle_offset=-1, match=m_cx) sim1.sample(circuit1, n_shots=100).plot() # replace any CZ cycle which follows a Hadamard cycle with a CNOT cycle circuit2 = tq.Circuit([cyc_cz, cyc_h, cyc_cz]) m_past = tqs.AndCycleMatch(m_h, m_cz) sim2 = tq.Simulator().add_cycle_noise(cyc_cx, match=m_past, cycle_offset=0) print(sim2.state(circuit2).mat()) # insert a cycle-like which does a small X rotation on qubit 0 and # depolarizes qubit 1 after any CNOT cycle superop = tqm.Superop.from_ptm(np.diag([1, 0.99, 0.99, 0.99])) cyc_like = {0: tq.Gate.rx(9), 1: superop} circuit3 = tq.Circuit([cyc_h, cyc_cx, cyc_h, cyc_cx]) sim3 = tq.Simulator().add_cycle_noise(cyc_like, cycle_offset=1, match=m_cx) mixed_state = sim3.state(circuit3) assert mixed_state.is_mixed # replace any CNOT cycle with a noisy version of it, using a function in # place of a cycle-like def two_qubit_error(cycle, all_labels): cycle_like = {} # loop through gates in given cycle and perturb them pert = tq.Gate.rp("ZZ", 5) for labels, gate in cycle.gates.items(): cycle_like[labels] = pert @ gate**1.05 @ pert.adj # loop through qubits idling in this cycle and add random phase noise idle_qubits = set(all_labels).difference(cycle.labels) rng = tq.settings.get_rng() for label in idle_qubits: cycle_like[label] = tq.Gate.rz(5 * rng.standard_normal()) return cycle_like sim4 = tq.Simulator() sim4.add_cycle_noise(two_qubit_error, cycle_offset=0, match=m_cx) pure_state = sim4.state(circuit3)
[0.5+0.j 0.5+0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0.5+0.j 0.5+0.j]
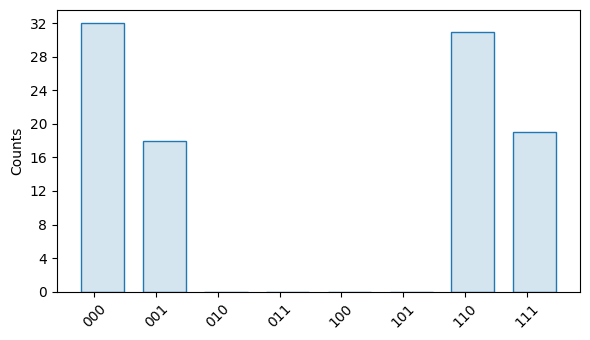
- Parameters:
replacement (
Cycle|dict|function) – ACycle-like, or a function which takes aCycle(and, optionally as a second argument, a tuple of all labels in the current circuit being simulated) and returns aCycle-like, to be inserted when the noise source matches.match (
BaseCycleMatch|NoneType) – A match object that specifies which cycles this noise source applies to.cycle_offset (
int) – Whether to insert the replacement cycle before (-1), in place of (0), or after (+1) the cycles matched by this noise source.
- Returns:
This simulator instance so that
add_*()calls can be chained.- Return type:
- Raises:
ValueError – If the match is not a cycle match instance, the
cycle_offsetis not-1,0or1, or ifreplace_withgenerates a cycle with invalid dimensions.
- add_depolarizing(p, local=True, match=None)
Appends a noise source to this simulator that adds isotropic depolarizing noise to the simulation. By default, noise is added every time a gate is encountered, however, by specifying
match, the user can design a noise profile which is gate- and/or qubit-dependent. SeeMatchfor more details.Depolarizing noise is applied to every system being acted on by a gate in a given cycle. For example, if qubits (0,1) get a CNOT, and qubit 3 gets an X in a given cycle, then depolarizing noise is applied to only these three qubits, even if the preceeding cycle contained a gate which acted on qubit 2. This noise source works for any subsystem dimension.
This noise source only applies noise—it does not try to implement the cycle in question, but only adds noise to it.
By default, if a two-qubit gate is encountered, then the tensor product of two one-qubit depolarizing channels will be applied to the two qubits the gate acts on, see the documentation of
depolarizing()and also the following example:import trueq as tq import trueq.simulation as tqs circuit = tq.Circuit([{(0, 1): tq.Gate.cx, 2: tq.Gate.h}]) # make a simulator with local depolarizing noise with a depolarizing # strength of p=0.02 applied to each single qubit a gate acts on sim = tq.Simulator().add_depolarizing(0.02) print(sim.sample(circuit, 1000)) # make a simulator where depolarizing noise acts only on locations where # gates act on qubit 5 sim = tq.Simulator().add_depolarizing(0.04, match=tqs.LabelMatch(5)) print(sim.sample(circuit, 1000))
Results({'000': 479, '001': 497, '010': 7, '011': 5, '110': 8, '111': 4}) Results({'000': 508, '001': 492})By setting
local=False, a global depolarizing channel is applied to all qubits that a matched gate acts on. That is, with respect to the formula above, we will have \(D=2\) for single qubit gates, \(D=4\) for two-qubit gates, \(D=27\) for three-qutrit gates, and so on. This is shown in the following example.import trueq as tq import trueq.simulation as tqs circuit = tq.Circuit([{(0, 1): tq.Gate(np.eye(4))}]) # make a simulator with depolarizing noise acting globally on each gate that # is found sim = tq.Simulator().add_depolarizing(0.02, local=False) tq.math.Superop(sim.operator(circuit).mat()).plot_ptm()
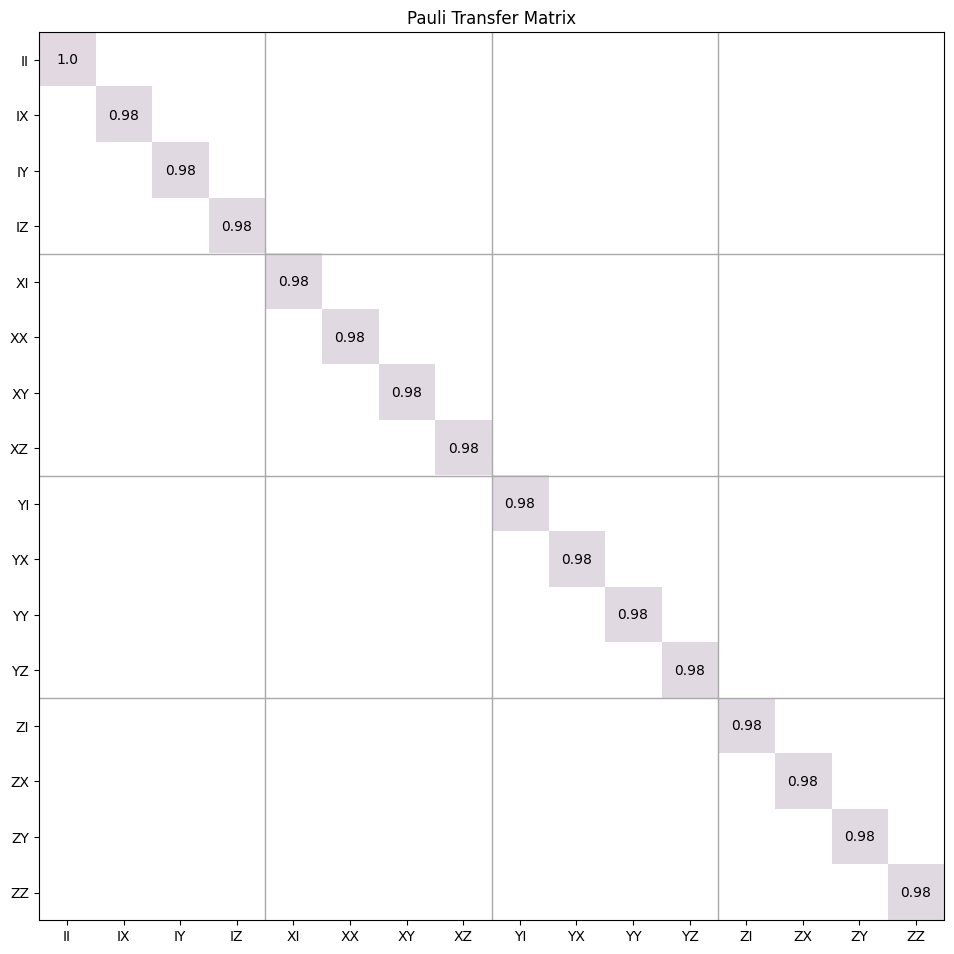
- Parameters:
p (
float) – The depolarizing parameter, as defined in the equation above.local (
bool) – Whether local depolarizing noise is applied to every qubit that is encountered on each matched gate, or whether global depolarizing noise is applied to all qubits encounterned on each matched gate.match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.
- Returns:
This simulator instance so that
add_*()calls can be chained.- Return type:
- add_gate_replace(fn, match=None)
Adds a noise source that replaces all matched
Gates in the circuit with the returned gate or superoperator of the provided functionfn. Each new gate-like object returned byfnmust act on the same dimensional subsystems as the gate it replaces.See below for an example of gate replacement noise, which overrotates native gates matching a specific name by a random value within \([-5, +5]\) degrees.
import trueq as tq import trueq.simulation as tqs import random def rand_noise(gate): # creates a small amount of random parameter noise. we use a match below # to guarantee any provided gate has a parameter called "theta" theta = gate.parameters["theta"] return tq.Gate.rp("X", theta + random.uniform(-5, 5)) # this match will ensure that ``rand_noise`` only ever applies to native # gates with the name "rx_noisy" match = tqs.NativeMatch("rx_noisy") # create and simulate a circuit with non-trivial noise application, where # any native gate with name "rx_noisy" also has a parameter named "theta" g = tq.NativeGate.from_generators("rx_noisy", "X", 90, params={"theta": 90}) circuit = tq.Circuit([{(0,): g}]) sim = tq.Simulator().add_gate_replace(rand_noise, match) # The 90 degree X rotation has been overrotated by a random amount sim.state(circuit).mat()
array([0.71310453+0.j , 0. -0.70105773j])
No caching is performed on the outputs of
fn; consider memoizing your function withfunctools.lru_cache()to increase speed.- Parameters:
- Returns:
This simulator instance so that
add_*()calls can be chained.- Return type:
- Raises:
ValueError – If the new gate does not match the dimensions of the gate that it is replacing.
- add_knr_noise(fit_or_circuits, exclusive=False, ignore_identity=False, ignore_marker=True)
A noise source which emulates the noise measured in a KNR experiment.
For each unique
Cyclewith results contained infit_or_circuits, we extract theNormalEstimates for each gate-body within the cycle. For each gate-body, we construct theSuperopwhich models the one-body noise, as measured by the KNR protocol.In the example below, we instantiate a noisy simulator and estimate the noise seen by an example cycle via the KNR protocol. We then use the resulting fit to instantiate a new simulator which reconstructs the noise of the first simulator.
import trueq as tq import trueq.simulation as tqs cycle = tq.Cycle({0: tq.Gate.h, 1: tq.Gate.z, (2, 3): tq.Gate.cx}) knr_circuits = tq.make_knr( cycle, n_random_cycles=[2, 6, 10], n_circuits=30, subsystems=1 ) sim = tq.Simulator().add_stochastic_pauli(px=0.01, py=0.01) sim.add_stochastic_pauli(pz=0.02, match=tqs.LabelMatch((0, 3))) sim.run(knr_circuits) knr_sim = tq.Simulator().add_knr_noise(knr_circuits) circuit = tq.Circuit(cycle) circuit.measure_all() knr_sim.sample(circuit, 100).plot() sim.sample(circuit, 100).plot()
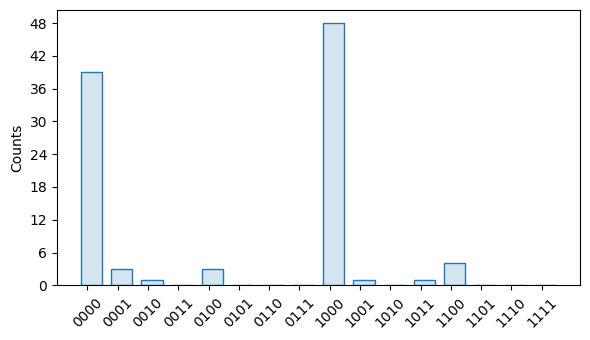
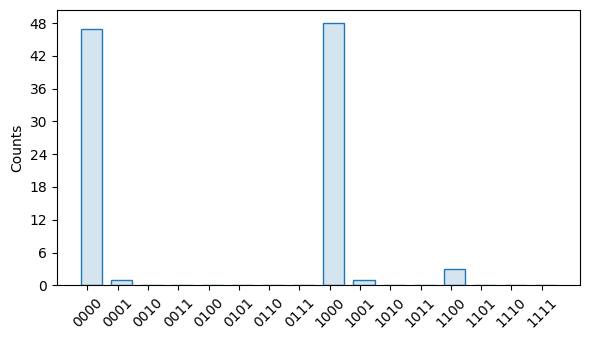
Running the KNR protocol on a cycle with explicitly defined identities will estimate the noise seen by idle qubits. For convenience, setting the flag
ignore_identitytoTruewill allow the reconstructed noise operator to match with cycles that do not contain explicit identity operators, so long as another cycle within the circuit being simulated contains operations which act on those qubits.Similarly, KNR noise can be set to apply to only those cycles which are equal to the cycle estimated by the KNR protocol and have equal marker values, by setting
ignore_markertoFalse. The matching occurs via an internally instantiatedCycleMatch.- Parameters:
fit_or_circuits (
EstimateCollection|CircuitCollection) – An estimate collection or a set of circuits which contain estimates of, or circuits for, the KNR protocol.exclusive (
bool) – IfTrue, all gates within the targeted cycles will be marked asno_more_noiseduring simulation. This isFalseby default.ignore_identity (
bool) – Whether or not to match this noise to cycles containing identical operations, ignoring any identity operators. This isFalseby default.ignore_marker (
bool) – IfTrue, match this noise to cycles which contain the same operations but have differet markers. This isTrueby default.
- Returns:
This simulator instance so that
add_*()calls can be chained.- Return type:
- Raises:
ValueError – If a cycle in the
fit_or_circuitsappears in the fit multiple times, or if the fit is empty.
- add_kraus(kraus_ops, match=None, dim=None)
Appends a noise source to this simulator that adds Kraus noise to the simulation. The noise is added to each gate matched by
match, so long as the Kraus operators’ dimensions allow it to be applied to the matched gates. Single-qubit Kraus noise will apply to all subsystems of any matched multi-qubit gate, whereas multi-qubit Kraus noise will only be applied to gates of the same dimension; this behaviour can be changed by using amatchwhich only matches single-qubit gates such asNQubitMatch. The noise map is defined by\[\mathcal{K}(\rho) = \sum_{i} K_i \rho K_i^\dagger\]Note that this applies only noise—it does not try to implement a given cycle in question, but only adds noise to it.
In every cycle, Kraus noise will only affect non-idling qubits. For example, if in a given cycle qubits
(0, 1)get a CNOT and no gate acts on qubit2, then Kraus noise is only applied to qubits(0, 1).import trueq as tq import trueq.simulation as tqs import numpy as np circuit = tq.Circuit([{(0, 1): tq.Gate.cx, 2: tq.Gate.h}]) # define qubit dephasing kraus operators kraus_ops = [np.sqrt(0.99) * np.eye(2), np.sqrt(0.01) * np.diag([1, -1])] # initialize a simulator in which qubit dephasing noise acts on every # location where gates are applied sim = tq.Simulator().add_kraus(kraus_ops) print(sim.sample(circuit, 1000)) # define a set of Kraus operators acting on single-qubit gates, and set # of Kraus operators to explicitly act on two-qubit gates kraus_ops1 = [np.sqrt(0.999) * np.eye(2), np.sqrt(0.001) * np.diag([1, -1])] kraus_ops2 = [ np.sqrt(0.99) * np.eye(4), np.sqrt(0.01) * np.fliplr(np.diag([1, 1, 1, 1])), ] # initialize a simulator with the noise defined above acting at # every location where a gate acts sim = tq.Simulator().add_kraus(kraus_ops1, match=tqs.SingleQubitMatch()) sim.add_kraus(kraus_ops2, match=tqs.NQubitMatch(2)) print(sim.sample(circuit, 1000)) # initialize a simulator which applies the above noise when a gate acts # on qubit 0 noisy_label = tqs.LabelMatch(0, strict=False) sim = tq.Simulator().add_kraus(kraus_ops1, match=noisy_label) sim.add_kraus(kraus_ops2, match=noisy_label) print(sim.sample(circuit, 1000)) # initialize a simulator which applies the above noise when an X gate acts # on qubit 2 or 3 # no 2 qubit gates will be matched under these conditions, no need to add # the two-qubit kraus channel to the simulator sim = tq.Simulator() noise_match = tqs.LabelMatch((2, 3)) & tqs.GateMatch(tq.Gate.x) sim.add_kraus(kraus_ops1, match=noise_match) print(sim.sample(circuit, 1000))
Results({'000': 511, '001': 489}) Results({'000': 505, '100': 1, '001': 491, '101': 3}) Results({'000': 499, '001': 489, '100': 7, '101': 5}) Results({'000': 485, '001': 515})- Parameters:
kraus_ops (
iterable) – An iterable of square matrices, each of which must be the same size, and act on subsystems of dimensiondim.match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.dim (
int|NoneType) – The dimension of each subsystem this Kraus operators act on, e.g.2for qubits. IfNone, this noise source will try to automatically infer the subsystem dimension by choosing the smallest compatible prime.
- Returns:
This simulator instance so that
add_*()calls can be chained.- Return type:
- Raises:
ValueError – If
kraus_opshas the wrong dimension or is not a list of square matrices.
- add_overrotation(single_sys=0, multi_sys=0, match=None)
Appends a noise source to this simulator that performs gate over/underrotation. This is done by propagating by the matrix power \(U_{err}=U^{(1+\epsilon)}\) instead of the ideal gate \(U\).
import trueq as tq import trueq.simulation as tqs circuit = tq.Circuit({(0, 1): tq.Gate.cx, 2: tq.Gate.h}) # initialize a simulator in which every single-qubit gate is overrotated by # epsilon=0.01 sim = tq.Simulator().add_overrotation(single_sys=0.01) print(sim.sample(circuit, 1000)) # initialize a simulator in which every single-qubit gate is overrotated by # epsilon=0.02 and every multi-qubit gate by epsilon=0.04 sim = tq.Simulator().add_overrotation(single_sys=0.02, multi_sys=0.04) print(sim.sample(circuit, 1000)) # initialize a simulator in which overrotations are applied whenever a gate # acts on any qubits in {0, 2} sim = tq.Simulator() noisy_labels = tqs.LabelMatch((0, 2)) sim.add_overrotation(single_sys=0.02, multi_sys=0.01, match=noisy_labels) print(sim.sample(circuit, 1000))
Results({'000': 480, '001': 520}) Results({'000': 474, '001': 526}) Results({'000': 527, '001': 473})- Parameters:
single_sys (
float) – The amount of over/underrotation to apply to gates that act on a single subsystem (ie. single-qubit). A value of0corresponds to no overrotation, a negative value corresponds to underrotation, and a positive value corresponds to overrotation.multi_sys (
float) – The amount of over/underrotation to apply to gates that act on a multiple subsystems (ie. multi-qubit). A value of0corresponds to no overrotation, a negative value corresponds to underrotation, and a positive value corresponds to overrotation.match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.
- Returns:
This simulator instance, so that
add_*()calls can be chained.- Return type:
- add_prep(default=0, states=None, match=None)
Appends a state preparation description to this simulator that chooses which state to prepare whenever a preparation instruction is encountered in a circuit.
A preparation state can be specified in any of the following formats:
A number between 0 and 1, representing a bitflip error probability of the ideal preparation \(|0\rangle\).
A length-\(d\) vector, representing the diagonal of a density matrix.
A length-\(d\) vector, representing a pure state.
A \(d\times d\) matrix, representing a density matrix.
If only one of the above is provided, it is used every time a
Prepobject is encountered. One can also specify that different subsystems get different errors by providing a dictionary mapping whose values are a combination of the above formats. See the examples below.The subsystem dimension is inferred automatically from the given
defaultandstates. When this is not possible, the value ofget_dim()is used.import trueq as tq circuit = tq.Circuit({i: tq.Prep() for i in range(3)}) # add 5% bitflip error to any qubit sim = tq.Simulator().add_prep(0.05) print(sim.sample(circuit, float("inf"))) # add 2% bitflip error by default, but 5% for qubits 1 and 2 sim = tq.Simulator().add_prep(0.02, {2: 0.05, 1: 0.05}) print(sim.sample(circuit, float("inf"))) # add specific density matrix to qubit 1, but 1% bitflip error by default sim = tq.Simulator().add_prep(0.01, {1: [[0.8, 0.1], [0.1, 0.2]]}) print(sim.sample(circuit, float("inf"))) # adding prep noise for qudits by using set dim tq.settings.set_dim(3) circuit = tq.Circuit({0: tq.Prep()}) # add 5% ditflip error to any qudit sim = tq.Simulator().add_prep(0.05) print(sim.sample(circuit, float("inf"))) tq.settings.set_dim(2)
Results({'000': 0.8573749999999999, '001': 0.045125, '010': 0.045125, '011': 0.0023750000000000004, '100': 0.045125, '101': 0.0023750000000000004, '110': 0.0023750000000000004, '111': 0.00012500000000000003}) Results({'000': 0.88445, '100': 0.01805, '001': 0.04655, '101': 0.00095, '010': 0.04655, '110': 0.00095, '011': 0.0024500000000000004, '111': 5.000000000000001e-05}) Results({'000': 0.78408, '001': 0.00792, '100': 0.00792, '101': 8e-05, '010': 0.19602, '011': 0.00198, '110': 0.00198, '111': 2e-05}) Results({'0': 0.95, '1': 0.025, '2': 0.025}, dim=3)For state simulation, if a
Prepoperator is encountered on a subsystem that has previously been initialized, then the register is traced out and the state is replaced with a new one.- Parameters:
state (
float|numpy.ndarray-like |dict) – A description of quantum states to initialize with.match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.
- Returns:
This simulator instance so that
add_*()calls can be chained.- Return type:
- Raises:
ValueError – If inconsistent dimensions are provided.
- add_rcal_noise(fit_or_circuits)
Appends measurement classification error to this simulator, where errors are specified by confusion matrices estimated by the readout calibration protocol (RCAL).
fit_or_circuitsshould be either a circuit collection with results from the RCAL protocol, or an estimate collection containing the fit for an RCAL estimate. If no RCAL fitting information is found, or if there are multiple fits present infit_or_circuits, an error will be raised.import trueq as tq import numpy as np # generate RCAL circuits to measure the readout errors on qubits [0, 1] circuits = tq.make_rcal([0, 1]) # initialize a mock device with a 20% readout error on every qubit sim = tq.Simulator().add_readout_error(0.2) # run the circuits on the mock device to populate their results and # estimate the readout error sim.run(circuits, n_shots=1000) fit = circuits.fit() # instantiate a simulator with the RCAL estimate and report the results # of running an example circuit with the new simulator sim = tq.Simulator().add_rcal_noise(fit) circuit = tq.Circuit({(0, 1): tq.Gate.x}).measure_all() sim.run(circuit, n_shots=np.inf) circuit.results.plot()
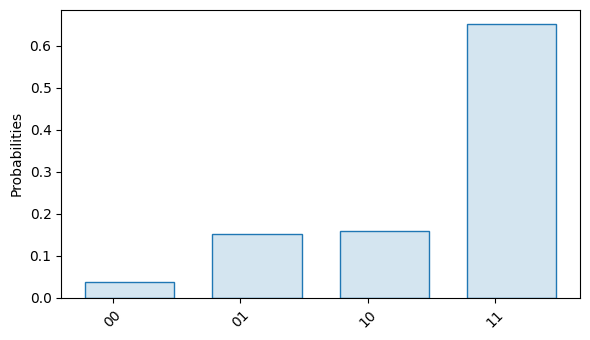
- Parameters:
fit_or_circuits (
EstimateCollection|CircuitCollection) – An estimate collection or a set of circuits which contain estimates of or circuits for the KNR protocol.- Raises:
ValueError – If
fit_or_circuitsdoes not contain exactly one RCAL estimate.- Returns:
This simulator instance so that
add_*()calls can be chained.- Return type:
- add_readout_error(default_error=0, errors=None, match=None)
Appends measurement classification error and/or positive operator valued measurement (POVM) error to this simulator.
For a qubit, a readout error of \(0.1\) will result in the confusion matrix \(\left(\begin{smallmatrix}0.9&0.1\\0.1&0.9\end{smallmatrix}\right)\), and the readout error of \((0.1, 0.02)\) in a confusion matrix \(\left(\begin{smallmatrix}0.9&0.0.2\\0.1&0.98\end{smallmatrix}\right)\). See
trueq.math.general.make_confusion_matrix()for more details about the allowed input formats for constructing confusion matrices.A POVM is specified as a 3D array \(E_{ijk}\) where each matrix \(E_i\) is positive semi-definite and encodes the probability of observing the \(i^{th}\) outcome. If \(\rho\) is the pre-measurement density matrix during simulation, then \(\operatorname{Tr}(\rho E_i)\) is the probability of outcome \(i\).
Errors can differ on individual qubits by singling out their labels in the second argument, see the example below. Similarly, correlated errors can be added by specifying larger confusion matrices and the qubits they act on.
The number of outcomes into which quantum states are classified does not need to match the subsystem dimension; confusion matrices can be rectangular so long as columns sum to unity.
The subsystem dimension and number of outcomes are inferred automatically from the given
default_erroranderrors. When this is not possible, the value ofget_dim()is used.import trueq as tq # make a test circuit that measures 4 qubits circuit = tq.Circuit([{range(4): tq.Meas()}]) # all qubits get 1% readout error sim = tq.Simulator().add_readout_error(0.01) print(sim.sample(circuit, 200)) # all qubits get 1% readout error, except qubit 1 gets 5% readout error sim = tq.Simulator().add_readout_error(0.01, {1: 0.05}) print(sim.sample(circuit, 200)) # all qubits get 1% readout error, except qubit 1 get 5% readout error, # and qubit 3 get asymmetric readout error of 1% on |0> and 7% on |1> sim = tq.Simulator().add_readout_error(0.01, {1: 0.05, 3: [0.01, 0.07]}) print(sim.sample(circuit, 200)) # we specify correlated measurement errors on qubits (3, 2) with a 4x4 # confusion matrix (row/column order is 00, 01, 10, 11). all other qubits # get 1% symmetric classification error. confusion = [ [0.81, 0.72, 0.72, 0.64], [0.09, 0.18, 0.08, 0.16], [0.06, 0.08, 0.18, 0.16], [0.04, 0.02, 0.02, 0.04], ] sim = tq.Simulator().add_readout_error(0.01, {(3, 2): confusion}) print(sim.sample(circuit, 200)) # here we add asymmetric qutrit classification error. the default error is # given as 0.02, so that for each i=0,1,2, a measurement |i> is # misclassified as |i+1> or |i+2> with probability 1% each. however, on # qubit 2, we have specified that |0> is reported as a '0' 99% of the time, # |1> is reported as a '1' 92% of the time, and |2> is reported as a '2' 80% # of the time. off-diagonals are the probabilities of misclassification # into specific outcomes corresponding to the row they are located in. we # add this error specifically to qutrit 2, the rest of the qutrits have # ideal measurements. confusion = [[0.99, 0.03, 0.02], [0.005, 0.92, 0.18], [0.005, 0.05, 0.8]] sim = tq.Simulator().add_readout_error(0.02, {2: confusion}) print(sim.sample(circuit, 200)) # classify qutrit measurements into binary outcomes. this situation arises, # for example, in superconducting qubits when there is leakage into the # third level of the anharmonic oscillator, but readout always reports a '0' # or a '1'. we use a rectangular confusion matrix where |2> is classified as # a '0' 70% of the time, and as a '1' 30% of the time. confusion = [[0.99, 0.08, 0.7], [0.01, 0.92, 0.3]] sim = tq.Simulator().add_readout_error(confusion) print(sim.sample(circuit, 200)) # use set dim for qudits when dimension is ambiguous tq.settings.set_dim(3) circuit = tq.Circuit({0: tq.Meas()}) sim = tq.Simulator().add_readout_error(0.05) print(sim.sample(circuit, float("inf"))) tq.settings.set_dim(2)
Results({'0000': 193, '0001': 1, '0010': 2, '0100': 3, '1000': 1}) Results({'0000': 187, '0001': 2, '0010': 1, '1000': 1, '0100': 9}) Results({'0000': 176, '0010': 1, '1000': 4, '0001': 3, '0100': 15, '0110': 1}) Results({'0000': 162, '0100': 1, '1000': 1, '0010': 15, '0001': 14, '0101': 1, '0011': 6}) Results({'0000': 191, '0001': 1, '0100': 1, '0200': 1, '1000': 2, '2000': 1, '0020': 2, '0021': 1}, dim=3) Results({'0000': 193, '0001': 1, '0010': 2, '0100': 2, '1000': 2}) Results({'0': 0.95, '1': 0.025, '2': 0.025}, dim=3)- Parameters:
default_error (
NoneType|numpy.ndarray-like |float) – Default readout error to be applied to all qubits that don’t receive special errors inerrors. Seetrueq.math.general.make_confusion_matrix()for the allowed input formats.errors (
dict) – A dictionary mapping qubit labels or tuples of qubit labels to any of the input formats allowed bydefault_error. Targeting multiple qubit labels in an entry allows for correlated readout error, though no qubit labels may overlap.match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.
- Returns:
This simulator instance so that
add_*()calls can be chained.- Return type:
- Raises:
ValueError – For any inconsistencies in the input arguments.
- add_relaxation(t1, t2, t_single, t_multi, excited_pop=0, match=None)
Appends a noise source to this simulator that adds \(T_1\) and \(T_2\) relaxation noise to the simulation. Specifically, for every cycle in a circuit, this noise source adds error to every qubit in the state defined by the Choi matrix:
\[\begin{split}C = \begin{pmatrix} 1-p(1-e^{-t/T_1}) & 0 & 0 & e^{-t/T_2} \\ 0 & (1-p)e^{-t/T_1} & 0 & 0 \\ 0 & 0 & pe^{-t/T_1} & 0 \\ e^{-t/T_2} & 0 & 0 & 1-(1-p)e^{-t/T_1} \end{pmatrix}\end{split}\]where \(t\) is the time of the longest gate in the cycle (i.e. either
t_singleort_multifor an entire cycle).import trueq circuit = tq.Circuit([{(0, 1): tq.Gate.cx, 2: tq.Gate.h}]) # make a simulator with relaxation noise with t1=100e-6, t2=50e-6, # single-qubit gate time 25e-9, two-qubit gate time 100e-9 and an excited # equilibrium population 0.01. sim = tq.Simulator().add_relaxation(100e-6, 50e-6, 25e-9, 100e-9, 0.01) print(sim.sample(circuit, 1000)) # make a simulator with relaxation noise with t1=10us, single-qubit gate # time 25ns and two-qubit gate time 100ns. t2=5us on all qubits except qubit # 0 which has t2=2.5us. t2 = {None: 5e-6, 0: 2.5e-6} sim = tq.Simulator().add_relaxation(10e-6, t2, 25e-9, 100e-9) # plot the final state tq.plot_mat(sim.state(circuit).mat())
Results({'000': 519, '001': 481})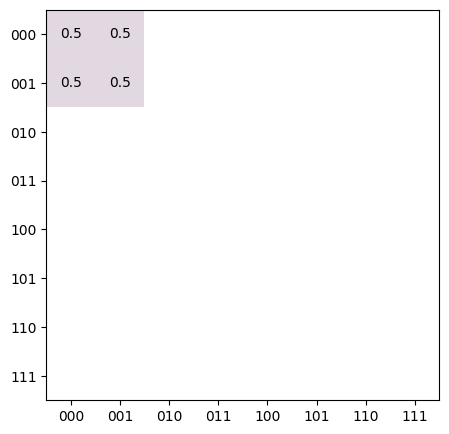
- Parameters:
t1 (
float|dict) – The \(T_1\) time, i.e. the characteristic time of relaxation. These can vary from qubit to qubit, see the example above.t2 (
float|dict) – The \(T_2\) time, i.e. the characteristic time of dephasing. These can vary from qubit to qubit, see the example above.t_single (
float) – The time it takes to perform a single-qubit gate.t_multi (
float) – The time it takes to perform a multi-qubit gate.excited_pop (
float|dict) – The excited state population at equilibrium.match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.
- Returns:
This simulator instance so that
add_*()calls can be chained.- Return type:
- Raises:
ValueError – If invalid \(T_1\) and \(T_2\) arguments are provided.
- add_stochastic_pauli(*, match=None, dim=None, **probabilities)
Appends a noise source to this simulator that introduces stochastic Pauli noise. This is done by applying superoperators with the Kraus representation
\[\mathcal{E}(\rho) = \sum{i}p_i P_i \rho P_i^\dagger\]for some probability vector \(p\), and where \(P_i\) are n-qubit Pauli operators (or n-qudit Weyl operators). Therefore, this method is a convenience wrapper for
add_superop()restricted to a certain family of superoperators. Note that this channel only applies noise—it does not try to implement the cycle in question, but only adds noise to it.Like
add_superop(), in the single-qubit case, this noise is applied to every system being acted on by a gate in a given cycle. For example, if qubits (0,1) get a CNOT, and qubit 3 gets an X in a given cycle, then stochastic Pauli noise is applied to only these three qubits, even if the preceeding cycle acted on qubit 2. Thematchargument can be used to specify under which conditions the stochastic Pauli noise should be applied, seeMatchfor more information.import numpy as np import trueq as tq circuit = tq.Circuit([{(0, 1): tq.Gate.cx, 2: tq.Gate.x, 3: tq.Gate.h}]) # initialize a simulator in which every location where a gate acts undergoes # Pauli noise with px=0.01 and py=0.04 sim = tq.Simulator().add_stochastic_pauli(px=0.01, py=0.04) print(sim.sample(circuit, 1000)) # initialize a simulator where every X gate undergoes Pauli noise with # py=pz=0 and px=0.04 noisy_gate = tqs.GateMatch(tq.Gate.x) sim = tq.Simulator().add_stochastic_pauli(px=0.04, match=noisy_gate) print(sim.sample(circuit, 1000)) # initialize a simulator with stochastic XX and YX noise on two-qubit gates sim = tq.Simulator().add_stochastic_pauli(XX=0.01, YX=0.05) print(sim.sample(circuit, 1000)) # initialize a simulator with stochastic W11 and W22 qutrit noise circuit = tq.Circuit({0: tq.Gate(np.diag([1, 1, -1]))}) sim = tq.Simulator().add_stochastic_pauli(W11=0.01, W22=0.02, dim=3) print(sim.sample(circuit, 1000))
Results({'0000': 33, '0001': 19, '0010': 388, '0011': 452, '0101': 3, '0110': 19, '0111': 25, '1010': 1, '1011': 1, '1100': 2, '1110': 26, '1111': 31}) Results({'0000': 16, '0001': 25, '0010': 455, '0011': 504}) Results({'0010': 454, '0011': 481, '1010': 37, '1011': 28}) Results({'0': 978, '1': 9, '2': 13}, dim=3)Note
The methods
add_stochastic_pauli()andadd_stochastic_weyl()are identical. They both exist to make searching the documentation easier.- Parameters:
match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.**probabilities – Keyword names describe which Pauli or Weyl error to introduce, and their value is the corresponding probability. The names can be Pauli or Weyl strings (see the constructor of
WeylBasefor allowed formats), orpx,py, andpzfor legacy support.
- Returns:
This simulator instance so that
add_*()calls can be chained.- Return type:
- Raises:
ValueError – If the probabilities do not sum to one, or any are negative.
ValueError – If the same Pauli/Weyl is specified in multiple ways.
ValueError – If different provided Pauli/Weyl strings represent different numbers of subsystems.
- add_stochastic_weyl(*, match=None, dim=None, **probabilities)
Appends a noise source to this simulator that introduces stochastic Pauli noise. This is done by applying superoperators with the Kraus representation
\[\mathcal{E}(\rho) = \sum{i}p_i P_i \rho P_i^\dagger\]for some probability vector \(p\), and where \(P_i\) are n-qubit Pauli operators (or n-qudit Weyl operators). Therefore, this method is a convenience wrapper for
add_superop()restricted to a certain family of superoperators. Note that this channel only applies noise—it does not try to implement the cycle in question, but only adds noise to it.Like
add_superop(), in the single-qubit case, this noise is applied to every system being acted on by a gate in a given cycle. For example, if qubits (0,1) get a CNOT, and qubit 3 gets an X in a given cycle, then stochastic Pauli noise is applied to only these three qubits, even if the preceeding cycle acted on qubit 2. Thematchargument can be used to specify under which conditions the stochastic Pauli noise should be applied, seeMatchfor more information.import numpy as np import trueq as tq circuit = tq.Circuit([{(0, 1): tq.Gate.cx, 2: tq.Gate.x, 3: tq.Gate.h}]) # initialize a simulator in which every location where a gate acts undergoes # Pauli noise with px=0.01 and py=0.04 sim = tq.Simulator().add_stochastic_pauli(px=0.01, py=0.04) print(sim.sample(circuit, 1000)) # initialize a simulator where every X gate undergoes Pauli noise with # py=pz=0 and px=0.04 noisy_gate = tqs.GateMatch(tq.Gate.x) sim = tq.Simulator().add_stochastic_pauli(px=0.04, match=noisy_gate) print(sim.sample(circuit, 1000)) # initialize a simulator with stochastic XX and YX noise on two-qubit gates sim = tq.Simulator().add_stochastic_pauli(XX=0.01, YX=0.05) print(sim.sample(circuit, 1000)) # initialize a simulator with stochastic W11 and W22 qutrit noise circuit = tq.Circuit({0: tq.Gate(np.diag([1, 1, -1]))}) sim = tq.Simulator().add_stochastic_pauli(W11=0.01, W22=0.02, dim=3) print(sim.sample(circuit, 1000))
Results({'0000': 27, '0001': 24, '0010': 438, '0011': 411, '0100': 1, '0101': 1, '0110': 25, '0111': 22, '1010': 1, '1100': 2, '1101': 2, '1110': 23, '1111': 23}) Results({'0000': 18, '0001': 26, '0010': 492, '0011': 464}) Results({'0010': 458, '0011': 487, '1010': 25, '1011': 30}) Results({'0': 968, '1': 12, '2': 20}, dim=3)Note
The methods
add_stochastic_pauli()andadd_stochastic_weyl()are identical. They both exist to make searching the documentation easier.- Parameters:
match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.**probabilities – Keyword names describe which Pauli or Weyl error to introduce, and their value is the corresponding probability. The names can be Pauli or Weyl strings (see the constructor of
WeylBasefor allowed formats), orpx,py, andpzfor legacy support.
- Returns:
This simulator instance so that
add_*()calls can be chained.- Return type:
- Raises:
ValueError – If the probabilities do not sum to one, or any are negative.
ValueError – If the same Pauli/Weyl is specified in multiple ways.
ValueError – If different provided Pauli/Weyl strings represent different numbers of subsystems.
- add_superop(superop, match=None)
Appends a noise source to this simulator that adds generic superoperator noise to the simulation. The noise is added to each gate matched by
matchwith an appropriate size. Specifically, single-qubit noise will apply to all subsystems of any matched multi-qubit gate, whereas multi-qubit noise will only be applied to gates of exactly the same dimension; this behaviour can be changed by using amatchwhich only matches single-qubit gates such asNQubitMatch.Note that this applies only noise—it does not try to implement a given cycle in question, but only adds noise to it.
In every cycle, noise will only affect non-idling qubits. For example, if in a given cycle qubits
(0, 1)get a CNOT and no gate acts on qubit2, then noise is only applied to qubits(0, 1).import trueq as tq import trueq.simulation as tqs import numpy as np circuit = tq.Circuit([{(0, 1): tq.Gate.cx, 2: tq.Gate.h}]) # choose a random superoperator with a process infidelity of 0.02 superop = tq.math.Superop.random_constrained_cptp(2, 0.02, 0.4) # initialize a simulator in which qubit noise acts on every # location where gates are applied sim = tq.Simulator().add_superop(superop) print(sim.sample(circuit, 1000)) # initialize a simulator where single qubits get one superoperator, # and two-qubit gates get another superop1 = tq.math.Superop.random_constrained_cptp(2, 0.01, 0.5) superop2 = tq.math.Superop.random_constrained_cptp(4, 0.04, 0.5) sim = tq.Simulator().add_superop(superop1, match=tqs.SingleQubitMatch()) sim.add_superop(superop2, match=tqs.NQubitMatch(2)) print(sim.sample(circuit, 1000))
Results({'000': 451, '001': 530, '010': 5, '011': 3, '110': 9, '111': 2}) Results({'000': 515, '010': 5, '100': 3, '110': 7, '001': 457, '011': 3, '101': 7, '111': 3})
- dressed_noise(cycle, n_randomizations=None, twirl='P', compiler=None, mix_orbits=True, probabilities=False)
Computes the dressed noise of the given cycle. The dressed noise is defined as
\[\tilde{\mathcal{E}} = \mathbb{E}[ \mathcal{T}^\dagger \mathcal{C}^\dagger \tilde{\mathcal{C}} \tilde{\mathcal{T}} ]\]where \(\mathcal{C}\) is the cycle of interest, \(\tilde{\mathcal{C}}\) its noisy simulation, \(\mathcal{T}\) an element of the twirling group, \(\tilde{\mathcal{T}}\) its noisy simulation, and where the expectation is taken uniformly over the twirling group.
The expectation value is taken in one of two ways. If
n_randomizations=None, twirling operations are assumed to be perfect so that the expectation value is a simple function of the diagonal elements of the superoperator \(\mathcal{C}^\dagger \tilde{\mathcal{C}}\) in the Pauli vectorization basis. Otherwise, the expectation is computed usingn_randomizationsMonte-Carlo samples from the twirling group, each of which is simulated with this simulator.Additionally, if
mix_orbits=True, error mixing via the orbit of the provided cycle is included. This mixing happens in practice during protocols like CB whose circuits consist of the cycle of interest repeated many times interleaved with samples of the twirling group. For instance, if a cycle contains a Hadamard, the effect of multiple dressed Hadamards back to back under Pauli twirling will result in the \(Z\) and \(X\) errors being mixed together. In particular, given the dressed noise \(\tilde{\mathcal{E}}\) defined above, the orbit-mixed error returned by this method is\[P[(\mathcal{C}\tilde{\mathcal{E}})^o]^{\frac{1}{o}}\]where \(o\) is such that \(\mathcal{C}^o \propto I\).
- Parameters:
cycle (
Cycle) – The cycle to find the dressed noise of.n_randomizations (
int|NoneType) – The number of random twirls to average over. IfNone, the twirling group is assumed to have a perfect implementation.twirl (
Twirl|str) – The twirling group to use.compiler (
Compiler) – A compiler to run all cycles through before simulating them.mix_orbits (
bool) – Whether to mix the dressed noise under the cycle.probabilities (
bool) – Whether to return the Pauli/Weyl probabilities of the noise channel as atrueq.math.tensor.Tensorinstead of the channel itself.
- Return type:
- predict_cb(cycle, labels=None, n_randomizations=50, targeted_errors=None, twirl='P', compiler=None)
Predicts the estimates that would be generated by simulating
make_cb()with this simulator.import trueq as tq sim = tq.Simulator().add_stochastic_pauli(px=0.01).add_overrotation(0.04) sim.predict_cb({0: tq.Gate.id, (1, 2): tq.Gate.cnot})
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".CBCycle BenchmarkingPaulis (0,) : Gate.id
(1, 2) : Gate.cx
- Key:
-
- cycles: (Cycle((0,): Gate.id, (1, 2): Gate.cx),)
- labels: (0, 1, 2)
- name:
- protocol: CB
- twirl: Paulis on [0, 1, 2]
${e}_{F}$The probability of an error acting on the specified labels during a dressed cycle of interest.6.7e-02 (0.0e+00) 0.06703529810826958, 0.0${e}_{III}$The probability of the subscripted error acting on the specified labels.9.3e-01 (0.0e+00) 0.9329647018917304, 0.0${p}_{ZZZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8933356435915776, 0.0${p}_{ZZY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8939044886209719, 0.0${p}_{ZZX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.1e-01 (0.0e+00) 0.9107796589968322, 0.0${p}_{ZZI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.1e-01 (0.0e+00) 0.9145298602812197, 0.0${p}_{ZYZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8924942387658985, 0.0${p}_{ZYY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.89249540931512, 0.0${p}_{ZYX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.1e-01 (0.0e+00) 0.9129409391198973, 0.0${p}_{ZYI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.1e-01 (0.0e+00) 0.9129409391198974, 0.0${p}_{ZXZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.89249540931512, 0.0${p}_{ZXY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8924942387658986, 0.0${p}_{ZXX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.9517975257425594, 0.0${p}_{ZXI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.9517975257425592, 0.0${p}_{ZIZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8933356435915776, 0.0${p}_{ZIY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8939044886209718, 0.0${p}_{ZIX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.9525401846304558, 0.0${p}_{ZII}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.6e-01 (0.0e+00) 0.9564620187540568, 0.0${p}_{YZZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.893618572435413, 0.0${p}_{YZY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8941875976240428, 0.0${p}_{YZX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.1e-01 (0.0e+00) 0.9110681125447874, 0.0${p}_{YZI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.1e-01 (0.0e+00) 0.9148195015575737, 0.0${p}_{YYZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8927769011279291, 0.0${p}_{YYY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8927780720478757, 0.0${p}_{YYX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.1e-01 (0.0e+00) 0.9132300771681191, 0.0${p}_{YYI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.1e-01 (0.0e+00) 0.9132300771681192, 0.0${p}_{YXZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8927780720478756, 0.0${p}_{YXY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.892776901127929, 0.0${p}_{YXX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.9520989700826069, 0.0${p}_{YXI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.9520989700826068, 0.0${p}_{YIZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8936185724354131, 0.0${p}_{YIY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.8.9e-01 (0.0e+00) 0.8941875976240429, 0.0${p}_{YIX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.952841864178426, 0.0${p}_{YII}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.6e-01 (0.0e+00) 0.9567649403883608, 0.0${p}_{XZZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9304649858761065, 0.0${p}_{XZY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9310574735777202, 0.0${p}_{XZX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.948634019725934, 0.0${p}_{XZI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.9525400890853535, 0.0${p}_{XYZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9295886100873895, 0.0${p}_{XYY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9295898292876672, 0.0${p}_{XYX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.9508851282466878, 0.0${p}_{XYI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.9508851282466877, 0.0${p}_{XXZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9295898292876675, 0.0${p}_{XXY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9295886100873899, 0.0${p}_{XXX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.9e-01 (0.0e+00) 0.9913566952130436, 0.0${p}_{XXI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.9e-01 (0.0e+00) 0.9913566952130436, 0.0${p}_{XIZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9304649858761069, 0.0${p}_{XIY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9310574735777205, 0.0${p}_{XIX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.9e-01 (0.0e+00) 0.9921302209271408, 0.0${p}_{XII}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.1.0e+00 (0.0e+00) 0.9962150566309461, 0.0${p}_{IZZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9340001234500509, 0.0${p}_{IZY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9345948622041681, 0.0${p}_{IZX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.9522381873388587, 0.0${p}_{IZI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.6e-01 (0.0e+00) 0.9561590971197539, 0.0${p}_{IYZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9331204180261226, 0.0${p}_{IYY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9331216418585366, 0.0${p}_{IYX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.954497848549327, 0.0${p}_{IYI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.5e-01 (0.0e+00) 0.954497848549327, 0.0${p}_{IXZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9331216418585369, 0.0${p}_{IXY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9331204180261229, 0.0${p}_{IXX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.1.0e+00 (0.0e+00) 0.9951231800949318, 0.0${p}_{IXI}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.1.0e+00 (0.0e+00) 0.9951231800949317, 0.0${p}_{IIZ}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.9340001234500507, 0.0${p}_{IIY}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.9.3e-01 (0.0e+00) 0.934594862204168, 0.0${p}_{IIX}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.1.0e+00 (0.0e+00) 0.9958996446835245, 0.0${p}_{III}$Decay parameter of the exponential decay $Ap^m$ for the given Pauli term.1.0e+00 (0.0e+00) 0.9999999999999958, 0.0- Parameters:
cycle (
dict|Cycle) – The cycle to make the prediction for.labels (
Iterable) – A list of which sets of system labels are to be twirled together in each circuit, e.g.[3, [1, 2], 4].n_randomizations (
int|NoneType) – The number of random twirls to average over. IfNone, the twirling group is assumed to have a perfect implementation.targeted_errors (
Iterable) – A list of Pauli strings, e.g.["ZIZIZ", "XYXYX"]that specify which errors to target. By default, the Pauli"I" * n_qubitsis used to estimate the probability of no error, i.e. the process fidelity.twirl (
Twirl|str) – The twirling group to use.compiler (
Compiler) – A compiler to run all cycles through before simulating them.
- Return type:
- Raises:
ValueError – If
targeted_errorsare not all Pauli strings of the correct length.
- predict_irb(cycle, n_randomizations=50, twirl='C', compiler=None)
Predicts the estimates that would be generated by simulating
make_irb()with this simulator.import trueq as tq sim = tq.Simulator().add_stochastic_pauli(px=0.01).add_overrotation(0, 0.1) sim.predict_irb({0: tq.Gate.id, (1, 2): tq.Gate.cnot})
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".IRBInterleaved Randomized BenchmarkingCliffords (0,) : Gate.id
(1, 2) : Gate.cx
- Key:
-
- cycles: (Cycle((0,): Gate.id, (1, 2): Gate.cx),)
- labels: (0,)
- name:
- protocol: IRB
- twirl: Cliffords on [0, (1, 2)]
Cliffords (0,) : Gate.id
(1, 2) : Gate.cx
- Key:
-
- cycles: (Cycle((0,): Gate.id, (1, 2): Gate.cx),)
- labels: (1, 2)
- name:
- protocol: IRB
- twirl: Cliffords on [0, (1, 2)]
${e}_{F}$The probability of an error acting on the targeted systems during a dressed gate of interest.2.0e-02 (0.0e+00) 0.019864000000000992, 0.07.8e-02 (0.0e+00) 0.07817187857256147, 0.0${p}$Decay parameter of the exponential decay $Ap^m$.9.7e-01 (0.0e+00) 0.9735146666666653, 0.09.2e-01 (0.0e+00) 0.9166166628559345, 0.0- Parameters:
cycle (
dict|Cycle) – The cycle to make the prediction for.n_randomizations (
int|NoneType) – The number of random twirls to average over. IfNone, the twirling group is assumed to have a perfect implementation.twirl (
Twirl|str) – The twirling group to use.compiler (
Compiler) – A compiler to run all cycles through before simulating them.
- Return type:
- predict_knr(cycle, subsystems=1, n_randomizations=50, twirl='P', compiler=None)
Predicts the estimates that would be generated by simulating
make_knr()with this simulator.import trueq as tq sim = tq.Simulator().add_stochastic_pauli(px=0.01).add_overrotation(0, 0.1) cycle = {0: tq.Gate.h, (1, 2): tq.Gate.cnot} prediction = sim.predict_knr(cycle, subsystems=2) prediction.plot.knr_heatmap()
- Parameters:
cycle (
dict|Cycle) – The cycle to make the prediction for.subsystems (
Iterable| :py:class`~trueq.Subsystems` |int) – A list of labels of combinations of gate-bodies to reconstruct the marginal probabilities for, which can be specified using aSubsystemsobject. Also accepts a positive integer to instantiate all combinations of gate bodies with up to and including that many elements.n_randomizations (
int|NoneType) – The number of random twirls to average over. IfNone, the twirling group is assumed to have a perfect implementation.twirl (
Twirl|str) – The twirling group to use.compiler (
Compiler) – A compiler to run all cycles through before simulating them.
- Return type:
- Raises:
ValueError – If a subsystem partially overlaps with one of the labels of the cycle.
- predict_srb(labels, n_randomizations=50, compiler=None)
Predicts the estimates that would be generated by simulating
make_srb()with this simulator.import trueq as tq sim = tq.Simulator().add_stochastic_pauli(px=0.01).add_overrotation(0.04) prediction = sim.predict_srb([0, [1, 2]]) prediction += sim.predict_srb([0]) prediction += sim.predict_srb([[1, 2]]) prediction.plot.compare_rb()

- Parameters:
labels (
Iterable|Twirl) – A list specifying sets of system labels to be twirled together by Clifford gates in each circuit, e.g.[3, [1, 2], 4]for mixed single and two-qubit twirling. Or, for advanced usage (including to specify a non-default dimension), aTwirlinstance.n_randomizations (
int|NoneType) – The number of random twirls to average over. IfNone, the twirling group is assumed to have a perfect implementation.compiler (
Compiler) – A compiler to run all cycles through before simulating them.
- Return type:
Simulation Backends
- class trueq.simulation.backend.SimulationBackend
Abstract parent class for all simulation backends. A instance of a subclass stores backend specific options and, when requested, constructs new
Runnerinstances, each of which can be used to simulate a single quantum circuit.- new_runner(prep_policy, meas_policy, dim, n_shots=inf)
Instantiates a new backend
Runnerthat can be used to simulate a single quantum circuit.- Parameters:
prep_policy (
PrepPolicy) – A policy specifying how to process preparation instructions.meas_policy (
MeasPolicy) – A policy specifying how to process measurement instructions.dim (
int) – The subsystem dimension to use during simulation.n_shots (
int) – The number of shots to sample if and when requested. This will only be relevant whenmeas_policyisRequireMeas.
- class Runner(prep_policy, meas_policy, dim, n_shots=inf)
An instance of a subclass performs the simulation of a single quantum circuit. Instructions are fed to a backend instance to be processed one at a time. The instance can either simulate it on the fly, or store instuctions and simulate when completed.
- Parameters:
prep_policy (
PrepPolicy) – A policy specifying how to process preparation instructions.meas_policy (
MeasPolicy) – A policy specifying how to process measurement instructions.dim (
int) – The subsystem dimension to use during simulation.n_shots (
int) – The number of shots to sample if and when requested. This will only be relevant whenmeas_policyisRequireMeas.
- property dim
The subsystem dimension this backend is using.
- Type:
int
- property meas_policy
The measurement policy used during simulation.
- Type:
- property n_shots
The number of shots to sample if and when requested. This will only be relevant when
meas_policyisRequireMeas.- Type:
int
- property prep_policy
The measurement policy used during simulation.
- Type:
- divide()
Instructs this backend that a new cycle of noise is about to begin. This exists in case it is helpful to a particular backend’s implementation; it should not affect the simulation result.
- process_confusion(labels, confusion)
Processes a confusion matrix instruction on the given labels.
- Parameters:
labels (
tuple) – The (ordered) labels on which the measurement acts.confusion (
numpy.ndarray) – A real array of shape(n_outcomes ** n, dim ** n)wheren = len(labels)and where each column sums to unity.
- process_gate(labels, gate)
Processes a single gate on the given labels.
- Parameters:
labels (
tuple) – The (ordered) labels on which the gate acts.gate (
Gate) – A gate whose shape is consistent with the labels and the dimension of this backend.
- process_meas(labels)
Processes an ideal measurement instruction on each of the given labels.
- Parameters:
labels (
tuple) – The labels on which the measurement acts.
- process_mixed_prep(labels, prep=None)
Processes a mixed state preparation instruction on the given labels.
- Parameters:
labels (
tuple) – The (ordered) labels on which the preparation acts.prep (
numpy.ndarray) – A density matrix with widthdim ** len(labels).
- process_prep(labels)
Processes an ideal preparation instruction on the given labels.
- Parameters:
labels (
tuple) – The labels on which the preparation acts.
- process_povm(labels, povm)
Processes a positive operator valued measurement instruction on the given labels.
- Parameters:
labels (
tuple) – The (ordered) labels on which the measurement acts.povm (
numpy.ndarray) – A complex array of shape(n_outcomes ** n, dim ** n, dim ** n)wheren = len(labels), and wherepovm[i]is the i’th POVM element in lexicographical order with respect to the order of the labels.
- process_pure_prep(labels, prep)
Processes a pure state preparation instruction on the given labels.
- Parameters:
labels (
tuple) – The (ordered) labels on which the preparation acts.prep (
numpy.ndarray) – A pure state with shapedim ** len(labels).
- process_superop(labels, superop)
Processes a single superoperator on the given labels.
- Parameters:
labels (
tuple) – The (ordered) labels on which the matrix acts.mat (
Superop) – A superoperator.
- property value
The final result of simulation. The type is completely dependent on the implementation.
- Type:
object
- class trueq.simulation.MeasPolicy(value)
Measurement policies for simulation backends.
- ForceDangling = 1
Ignore measurement instructions.
This policy is used to force a backend to compute the quantum state or operator of a circuit that contains measurement instructions.
Note
In the edge case that a measurement instruction is applied to a subsystem that hasn’t been addressed yet, a backend should include the label of the measurement in the simulation so that the total number of systems is consistent with that of the circuit.
This policy may be nonsensical for circuits with mid-circuit measurements; it is up to each backend type to raise appropriate errors or warnings.
- RequireMeas = 2
If no measurement instructions are specified in the circuit, finish the simulation by processing a measurement instruction on every qubit. Otherwise, process measurement instructions just as they appear.
This policy is used to allow a backend to sample outcomes from circuits irrespective of whether they were provided with measurement instructions.
- class trueq.simulation.PrepPolicy(value)
Preparation policies for simulation backends.
- ForceDangling = 1
Ignore preparation instructions.
This policy is typically used in conjugation with
MeasPolicy.ForceDanglingto force a backend to compute the total operator (unitary or superoperator) of a circuit that contains preparation instructions.Note
In the edge case that a preparation instruction is applied to a subsystem that hasn’t been addressed yet, a backend should include the label of the preparation in the simulation so that the total number of systems is consintent with that of the circuit.
- ForcePrep = 2
Whenever a new qubit label is first encountered with a non-preparation instruction, preceed it by an ideal preparation instruction.
This policy is used to allow a backend to simulate quantum states of circuits, or sample outcomes from circuits, irrespective of whether they begin with preparation instructions.
- class trueq.simulation.PropagationBackend
A simulation backend that uses
OperatorTensororStateTensorto perform simulations.- class Runner(prep_policy, meas_policy, dim, n_shots=inf)
Instantiates a
OperatorTensororStateTensorduring construction and mutates it through the course of a simulation.- Parameters:
prep_policy (
PrepPolicy) – A policy specifying how to process preparation instructions.meas_policy (
MeasPolicy) – A policy specifying how to process measurement instructions.dim (
int) – The subsystem dimension to use during simulation.n_shots (
int) – The number of shots to sample if and when requested. This is only relevant whenmeas_policyisRequireMeas.
- property meas_labels
All of the labels that explicitly received a
Measinstruction.- Return type:
tuple
- process_gate(labels, gate)
Processes a single gate on the given labels.
- Parameters:
labels (
tuple) – The (ordered) labels on which the gate acts.gate (
Gate) – A gate whose shape is consistent with the labels and the dimension of this backend.
- process_meas(labels, error=0)
Processes an ideal measurement instruction on each of the given labels.
- Parameters:
labels (
tuple) – The labels on which the measurement acts.
- process_povm(labels, error=0)
Processes an ideal measurement instruction on each of the given labels.
- Parameters:
labels (
tuple) – The labels on which the measurement acts.
- process_confusion(labels, error=0)
Processes a measurement instruction with errors on the given labels.
- Parameters:
labels (
tuple) – The (ordered) labels on which the measurement acts.error (
numpy.ndarray) – A 2D matrix specifying a real confusion matrix or a 3D complex array specifying a POVM.
- process_prep(labels, prep=None)
Processes an ideal preparation instruction on the given labels.
- Parameters:
labels (
tuple) – The labels on which the preparation acts.
- process_pure_prep(labels, prep=None)
Processes an ideal preparation instruction on the given labels.
- Parameters:
labels (
tuple) – The labels on which the preparation acts.
- process_mixed_prep(labels, prep=None)
Processes a preparation instruction on the given labels.
- Parameters:
labels (
tuple) – The labels on which the preparation acts.prep (
numpy.ndarray) – The pure state or mixed state to prepare on the given labels.
- property dim
The subsystem dimension this backend is using.
- Type:
int
- divide()
Instructs this backend that a new cycle of noise is about to begin. This exists in case it is helpful to a particular backend’s implementation; it should not affect the simulation result.
- property meas_policy
The measurement policy used during simulation.
- Type:
- property n_shots
The number of shots to sample if and when requested. This will only be relevant when
meas_policyisRequireMeas.- Type:
int
- property prep_policy
The measurement policy used during simulation.
- Type:
- new_runner(prep_policy, meas_policy, dim, n_shots=inf)
Instantiates a new backend
Runnerthat can be used to simulate a single quantum circuit.- Parameters:
prep_policy (
PrepPolicy) – A policy specifying how to process preparation instructions.meas_policy (
MeasPolicy) – A policy specifying how to process measurement instructions.dim (
int) – The subsystem dimension to use during simulation.n_shots (
int) – The number of shots to sample if and when requested. This will only be relevant whenmeas_policyisRequireMeas.
Match
- class trueq.simulation.match.Match(exclusive=False)
A class whose purpose is to filter the operations presented to a given
NoiseSourcein aSimulatorinstance. This is typically used by a noise source to specify, for example, which gate, label, and cycle combinations to apply noise to. This base class is a pass-through that does not do any filtering except the following which is common to all noise sources:Any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
The match also defines
iter_*functions, which are called byNoiseSources, and return an iterator of pairs ofOperations and labels (tuples). The noise source function called during propagation,apply(), does not calliter()directly, which returns an iterator ofOpWrappers, but instead calls to the match via theiter_*wrapper functions, meaning that aNoiseSourcedoes not (and should not) need to interact with aOpWrapper.Two or more matches can be joined together with
&(AndMatch) and|(OrMatch) that restrict operations to the intersection of matches, or the union of matches, respectively. This is seen in the following examples:import trueq as tq import trueq.simulation as tqs # Create a match that matches only X gates. noisy_x = tqs.GateMatch(tq.Gate.x) # Create a match that matches only Y gates. noisy_y = tqs.GateMatch(tq.Gate.y) # Create a match that matches any operation acting on a subset of labels # (2, 4). noisy_labels = tqs.LabelMatch((2, 4)) # Single label matches can send in the label as an integer instead of a tuple # of length 1. This match matches all operations on qubit 0. zero_match = tqs.LabelMatch(0) # A match which prevents subsequent noise sources from seeing operations # that are matched with this one. no_more_match = tqs.Match(exclusive=True) # Create a match that restricts to X gates and any gate on qubits 2 and 4 noise_restriction = tqs.OrMatch(noisy_x, noisy_labels) # Equivalently, we can use ``|`` noise_restriction = noisy_x | noisy_labels # Create a match that restricts to X gates only on qubits 2 and 4 noise_restriction = tqs.AndMatch(noisy_x, noisy_labels) # Equivalently, we can use ``&`` noise_restriction = noisy_x & noisy_labels # Create a match that restricts to Y gates on qubits 2 and 4, and any X gates compound_match = (noisy_y & noisy_labels) | noisy_x # The following produce equivalent match behaviour: equiv1 = noisy_x | noisy_y equiv2 = tqs.GateMatch([tq.Gate.x, tq.Gate.y])
- iter(op_type, cycle_wrappers, noise_only=True, update_flags=True)
Iterates through the operations in the most recent cycle in
cycle_wrappers, yielding every operation of typeop_typethat is matched by this instance and that has not yet been marked for no further simulation viaOpwrapper.no_more_noise.- Parameters:
op_type (
Gate|Meas|Prep) – The type ofOperationto extract from thecycle_wrapper.cycle_wrappers (
list) – A list ofCycleWrappers, with the last one being the most recent.noise_only (
bool) – Whether to mark theOpWrapperashas_been_simulatedafter it has been yielded.update_flags (
bool) – Whether to mutateOpWrapperflags when an operation is yielded. Only composite matches such asAndMatchshould consider setting this toFalse.
- Returns:
An iterator of
OpWrappers with operations of typeop_type- Return type:
Iterable
- iter_gates(cycle_wrappers, noise_only=True)
Yields pairs
(labels, gate)in the most recent cycle incycle_wrapperswheregateis aGatethat is matched by this instance.- Parameters:
cycle_wrappers (
list) – A list ofCycleWrappers, with the last one being the most recent.noise_only (
bool) – Whether to mark theOpWrapperashas_been_simulatedafter it has been yielded.
- Returns:
An iterator of labels and operators.
- Return type:
Iterable
- iter_meas(cycle_wrappers, noise_only=True)
Yields pairs
(labels, meas)in the most recent cycle incycle_wrapperswheremeasis aMeasthat is matched by this instance.- Parameters:
cycle_wrappers (
list) – A list ofCycleWrappers, with the last one being the most recent.noise_only (
bool) – Whether to mark theOpWrapperashas_been_simulatedafter it has been yielded.
- Returns:
An iterator of labels and operators.
- Return type:
Iterable
- iter_prep(cycle_wrappers, noise_only=True)
Yields pairs
(labels, prep)in the most recent cycle incycle_wrapperswhereprepis aPrepthat is matched by this instance.- Parameters:
cycle_wrappers (
list) – A list ofCycleWrappers, with the last one being the most recent.noise_only (
bool) – Whether to mark theOpWrapperashas_been_simulatedafter it has been yielded.
- Returns:
An iterator of labels and operators.
- Return type:
Iterable
- class trueq.simulation.match.AndMatch(*matches, exclusive=None)
Instances of this class match operations that match the intersection of the given
matches. Operations are matched as follows:Any operation that matches all of the given
matches.However, any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
- class trueq.simulation.match.AssociativeMatch(*matches, exclusive=None)
Abstract parent class for children
Cthat stores a list ofMatches and have the property thatC([A, C([B, C]))andC([A, B, C])share the same behaviour. This flattening process is performed automatically by the constructor whenAssociativeMatches of the same type are encountered.
- class trueq.simulation.match.GateMatch(gates, exclusive=False)
Instances of this class match a fixed set of gates. Operations are matched as follows:
Any gate in
gates.However, any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
- class trueq.simulation.match.LabelMatch(labels, strict=True, exclusive=False)
Instances of this class match operations whose qubit labels correspond to a specified set of labels. Operations are matched as follows:
If
strictis true, operations whose labels are a strict subset of this instance’s labels are yielded.If
strictisFalse, operations whose labels have some intersection with this instance’s labels are yielded.However, any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
For example, a
LabelMatchinitialized with the label 0 will match to single-qubit operations on label 0, regardless of the value ofstrict. IfstrictisFalse, it will also match to any multi-qubit operations on label 0, like a CNOT gate over labels 0 and 1.- Parameters:
labels (
tuple) – A tuple of integers representing the labels to be matched.strict (
bool) – Determines if label matching is performed by subset or by intersection.exclusive (
bool) – Whether to mark every operation yielded during iteration asno_more_noise. In any future iterations by anyMatchan operation with this marking will be skipped.
- class trueq.simulation.match.NQubitMatch(n_sys, exclusive=False)
Instances of this class match operations that act on only
n_sysqubit labels. Operations are matched as follows:All operations that act on a
n_sysqubit labels.Any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
- Parameters:
n_sys (
int) – An integer defining the number of qubit labels upon which an operator must act on order to be matched by this instance.exclusive (
bool) – Whether to mark every operation yielded during iteration asno_more_noise. In any future iterations by anyMatchan operation with this marking will be skipped.
- class trueq.simulation.match.NativeMatch(name, exclusive=False)
Instances of this class match operations that are
NativeGates with a specifiedname. Operations are matched as follows:Any native gate with a name that matches
nameis returned.However, any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
The following example showcases this behaviour:
import trueq as tq import trueq.simulation as tqs # match all native gates with the name "rz" match = tqs.NativeMatch("rz")
- Parameters:
name – A string for matching to names of native gates.
exclusive (
bool) – Whether to mark every operation yielded during iteration asno_more_noise. In any future iterations by anyMatchan operation with this marking will be skipped.
- class trueq.simulation.match.OrMatch(*matches, exclusive=None)
Instances of this class match operations that match the union of the specified set of
matches. Operations are matched as follows:Any operation that matches any of the given
matches.However, any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
- class trueq.simulation.match.R90Match(exclusive=False)
Instances of this class match qubit gates that can be represented as a 90 degree rotation about an axis within the XY plane. Operations are matched as follows:
Any qubit gate that is a 90 degree rotation about an axis within the XY plane.
However, any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
- Parameters:
exclusive (
bool) – Whether to mark every operation yielded during iteration asno_more_noise. In any future iterations by anyMatchan operation with this marking will be skipped.- Raises:
RuntimeError – Throws an error if the cycle is not from a qubit circuit.
- class trueq.simulation.match.SingleQubitMatch(exclusive=False)
Instances of this class match operations that act on only a single qubit label. Operations are matched as follows:
All operations that act on a single qubit label.
However, any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
- Parameters:
exclusive (
bool) – Whether to mark every operation yielded during iteration asno_more_noise. In any future iterations by anyMatchan operation with this marking will be skipped.
NoiseSource
- class trueq.simulation.noise_source.NoiseSource(match=None, dim=None)
Parent class for all built in noise sources which can be added to the simulator.
A noise source comprises a method
apply()that mutates the state of simulation by inspecting a given cycle, aMatchinstance for filtering which operations in the cycle to consider, a cache for storing saved calculations that persists for the lifetime of the noise source, and an optional attributedimfor explicitly defining the allowed subsystem dimension.Generally, a
NoiseSourceis added to a simulator, and then during circuit propagation it has an opportunity to apply noise cycle by cycle. Within the simulation of each cycle, a noise source can either simply add noise, or additionally attempt to simulate some of the operations within a cycle. A default noise source is always included in theSimulatorto ensure that all gates within a cycle that are not simulated by a user-appended noise source are eventually simulated ideally.- Parameters:
match (
Match|NoneType) – A match object which determines the conditions required for a noise source to attempt to apply itself to the state during simulation.dim (
int|NoneType) – The subspace dimension expected by a noise source, orNone, if there is no needed restriction to a particular subspace dimension.
- property dim
The Hilbert space dimension of each subsystem expected by this propagator. If the dimension is set to
None, then the noise source does not care about the dimension of a given subsystem. Otherwise, the dimension is an integer, and the noise source can use this information to assert that it can be applied correctly during simulation.- Returns:
The expected dimension of subsystems as an integer, or
None.- Type:
int|NoneType
- property match
The
Matchinstance owned by this noise source. This object is typically used byapply()to filter which cycle operations are presented to it.For example, the noise source can be initialized with a match on gates, defined by an instance of
GateMatchinitialized with a list of gates. In this case, the noise source will only have the opportunity to apply itself to the state whenever one of these gates appears.
- make_circuit_cache(circuit)
Instantiates a cache object that will be made available to
apply()ascircuit_cachefor each call within the circuit. The cache is typically a dictionary that stores information about the circuit that is needed byapply()but not available in individual cycles of the circuit, such as all of the labels the circuit acts on.- Parameters:
circuit (
Circuit) – The circuit being simulated by the (noisy) simulator.- Returns:
A dictionary of circuit information.
- Return type:
dict
- apply(cycle_wrappers, backend, circuit_cache)
Processes all operations in the last of the given
cycle_wrappersthat have not yet been completely processed by the given backend. This method defines ideal simulation, which children will typically overload to add noise.- Parameters:
cycle_wrappers (
list) – AllCycleWrappers from the beginning of the circuit up until the current cycle in the simulation. These are all given to allow non-Markovian noise; typically only the last will be used.backend (
Runner) – The simulation backend.circuit_cache (
dict) – Cached information about the circuit.
- class trueq.simulation.add_basic.DepolarizingNoise(p, local, match=None)
A noise source that adds depolarizing noise; see
add_depolarizing()for details.- Parameters:
p (
float) – The depolarizing parameter, as defined in the above referenced function.local (
bool) – Whether local depolarizing noise is applied to every qubit that is encountered on each matched gate, or whether global depolarizing noise is applied to all qubits encounterned on each matched gate.match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.
- apply(cycle_wrappers, backend, cache)
Allows the backend to process the depolarizing noise.
- Parameters:
cycle_wrappers (
list) – AllCycleWrappers from the beginning of the circuit up until the current cycle in the simulation. This noise source only uses the last one.backend (
Runner) – The simulation backend.cache (
dict) – A dictionary to cache results in.
- class trueq.simulation.add_basic.GateReplaceNoise(fn, match=None)
A noise source that replaces all valid
Gates present in the circuit with the returned valued offn; seeadd_gate_replace()for details.- Parameters:
- Raises:
ValueError – If the new gate does not match the dimensions of the gate that it is replacing.
- apply(cycle_wrappers, backend, cache)
Allows the backend to process the gate replacement noise.
- Parameters:
cycle_wrappers (
list) – AllCycleWrappers from the beginning of the circuit up until the current cycle in the simulation. This noise source only uses the last one.backend (
Runner) – The simulation backend.cache (
dict) – A dictionary to cache results in.
- Raises:
ValueError – If the new gate-like object does not act on the same dimensional subsystems as the gate that it is replacing.
- class trueq.simulation.add_basic.OverrotationNoise(single_sys, multi_sys, match=None)
A noise source that adds unitary overrotation error; see
add_overrotation()for details.- Parameters:
single_sys (
float) – The amount of overrotation to add to single-qubit gates..multi_sys (
float) – The amount of overrotation to add to multi-qubit gates.match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.
- apply(cycle_wrappers, backend, cache)
Allows the backend to process the overrotation noise.
- Parameters:
cycle_wrappers (
list) – AllCycleWrappers from the beginning of the circuit up until the current cycle in the simulation. This noise source only uses the last one.backend (
Runner) – The simulation backend.cache (
dict) – A dictionary to cache results in.
- class trueq.simulation.add_basic.RelaxationNoise(t1, t2, t_single, t_multi, excited_pop=0, match=None)
A noise source that adds relaxation noise, a noise restricted to qubits; see
add_relaxation()for details.Relaxation noise simulates a \(T_1\) and \(T_2\) process on the qubits, in an idealized manner assuming that gates happen instantaneously, and that the relaxation occurs before any ideal operation is simulated.
- Parameters:
t1 (
float|dict) – The \(T_1\) time, i.e. the characteristic time of relaxation.t2 (
float|dict) – The \(T_2\) time, i.e. the characteristic time of dephasing.t_single (
float) – The idealized time it takes for single-qubit cycles to run.t_multi (
float) – The idealized time it takes for multi-qubit cycles to run.excited_pop (
float|dict) – The excited state population at equilibrium.match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.
- make_circuit_cache(circuit)
Instantiates a cache object that will be made available to
apply().- Parameters:
circuit (
Circuit) – The circuit being simulated.- Returns:
All of the labels the circuit acts on.
- Return type:
tuple
- static relaxation_channel(t1, t2, t, excited_pop)
Determines and returns the superoperator for a relaxation channel by computing the Choi representation, and casting it to a superoperator.
- Parameters:
t1 (
float|dict) – The \(T_1\) time, i.e. the characteristic time of relaxation.t2 (
float|dict) – The \(T_2\) time, i.e. the characteristic time of dephasing.t (
float) – The time that the channel is applied for.excited_pop (
float|dict) – The excited state population at equilibrium.
- Return type:
- Raises:
ValueError – Raises when \(T_1\) and \(T_2\) are physically invalid, or if
excited_popis a not a valid probability.
- apply(cycle_wrappers, state, cache)
Allows the backend to process the relaxation noise.
- Parameters:
cycle_wrappers (
list) – AllCycleWrappers from the beginning of the circuit up until the current cycle in the simulation. This noise source only uses the last one.backend (
Runner) – The simulation backend.cache (
dict) – A dictionary to cache results in.
- class trueq.simulation.add_basic.SuperopNoise(superop, match=None)
A noise source that adds superoperator noise; see
add_superop()for details.- Parameters:
- apply(cycle_wrappers, backend, cache)
Allows the backend to process the superoperator noise.
- Parameters:
cycle_wrappers (
list) – AllCycleWrappers from the beginning of the circuit up until the current cycle in the simulation. This noise source only uses the last one.backend (
Runner) – The backend to propagate.cache (
dict) – A dictionary to cache results in.
- Raises:
ValueError – If a multi-qubit superoperator matches to a multi-qubit gate with a larger dimension.
- class trueq.simulation.add_cycle_noise.CycleReplacementNoise(replacement, match, cycle_offset=0)
A noise source which inserts or replaces entire cycles during simulation; see
add_cycle_noise()for more information.- Parameters:
replacement (
Cycle|dict|function) – ACycle-like, or a function which takes aCycle(and, optionally as a second argument, a tuple of all labels in the current circuit being simulated) and returns aCycle-like, to be inserted when the noise source matches.match (
BaseCycleMatch|NoneType) – A match object that specifies which cycles this noise source applies to.cycle_offset (
int) – Whether to insert the replacement cycle before (-1), in place of (0), or after (+1) the cycles matched by this noise source.
- Raises:
ValueError – If the match is not a cycle match instance, the
cycle_offsetis not-1,0, or1, or ifreplacementgenerates a cycle with invalid dimensions.
- make_circuit_cache(circuit)
Caches the circuit labels to be used during
apply().- Parameters:
circuit (
Circuit) – The circuit being simulated by the (noisy) simulator.- Return type:
tuple
- apply(cycle_wrappers, backend, cache)
Allows the backend to process the replacement noise.
- Parameters:
cycle_wrappers (
list) – AllCycleWrappers from the beginning of the circuit up until the current cycle in the simulation.backend (
Runner) – The simulation backend.cache (
dict) – A dictionary to cache results in.
- class trueq.simulation.add_cycle_noise.KNRNoise(fit_or_circuits, exclusive=False, ignore_identity=False, ignore_marker=True)
A noise source which reconstructs the noise of each cycle for each KNR experiment in
fit_or_circuits; see the KNR guide andadd_knr_noise()for details.- Parameters:
fit_or_circuits (
EstimateCollection|CircuitCollection) – An estimate collection or a set of circuits which contain estimates of, or circuits for, the KNR protocol.exclusive (
bool) – IfTrue, all gates within the targeted cycles will be marked asno_more_noiseduring simulation. This isFalseby default.ignore_identity (
bool) – Whether or not to match this noise to cycles containing identical operations, ignoring any identity operators. This isFalseby default.ignore_marker (
bool) – IfTrue, match this noise to cycles which contain the same operations but have differet markers. This isTrueby default.
- Raises:
ValueError – If a cycle in the
fit_or_circuitsappears in the fit multiple times, or if the fit is empty.
- static knr_superop(estimate)
Returns a
Superoprepresenting the one-body noise acting on the gate-body estimated byestimate, as fitted by the KNR protocol.- Parameters:
estimate (
NormalEstimate) – The estimate containing the fit information for the gate-body.- Returns:
The reconstructed superoperator for the KNR estimate.
- Return type:
- apply(cycle_wrappers, backend, cache)
Allows the backend to process the KNR noise.
- Parameters:
cycle_wrappers (
list) – AllCycleWrappers from the beginning of the circuit up until the current cycle in the simulation. This noise source only uses the last one.backend (
Runner) – The simulation backend.cache (
dict) – A dictionary to cache results in.
- class trueq.simulation.add_spam.PrepNoise(default, custom, match)
A noise source that adds state preparation error; see
add_prep()for details.
- class trueq.simulation.add_spam.ReadoutNoise(default, custom, match)
A noise source that adds readout error; see
add_readout_error()for details.
- class trueq.simulation.add_spam.SpamNoise(default, custom, match)
Abstract parent class for state preparation and measurement (SPAM) noise sources.
- Parameters:
default (
object) – The default SPAM noise to apply.custom (
dict) – A dictionary mapping qubit labels or label tuples to SPAM noise.match (
Match|NoneType) – A match object that specifies which operations or cycles this noise source applies to.
- apply(cycle_wrappers, backend, cache)
Allows the backend to process this SPAM noise.
- Parameters:
cycle_wrappers (
list) – AllCycleWrappers from the beginning of the circuit up until the current cycle in the simulation. This noise source only uses the last one.backend (
Runner) – The simulation backend.cache (
dict) – A dictionary to cache results in.
Cycle Matches
- class trueq.simulation.match.BaseCycleMatch(lag=0, exclusive=False)
Abstract parent class for children that match against all operations in a
Cycleas a whole, rather than single operations at a time. Children of this class can specify custom cycle matching functions by overwritingcheck_match(). Two or more matches can be joined together with&(AndCycleMatch) and|(OrCycleMatch) that restrict operations to the intersection of matches, or the union of matches, respectively. Cycle matches can be initialized such that they match on the past cycles via thelagparameter, allowing for the possibility of non-Markovian noise.import trueq as tq import trueq.simulation as tqs cyc_h = tq.Cycle({0: tq.Gate.h}) cyc_cx = tq.Cycle({(0, 1): tq.Gate.cx}) cyc_cx_alt = tq.Cycle({(0, 2): tq.Gate.cx}) # create a match which matches if the previous cycle was ``cyc_h`` m_past = tqs.CycleMatch(cyc_h, lag=1) # create a match which matches if the current cycle is ``cyc_cx`` m_present = tqs.CycleMatch(cyc_cx) # create equivalent matches which match if the previous cycle was ``cyc_h`` # and the current cycle is ``cyc_cx`` m_joint = m_past & m_present m_joint_alt = tqs.AndCycleMatch(m_past, m_present) # create a match which matches if the previous cycle was an H gate on # ``0`` and the current cycle is a CNOT on either ``(0,1)`` or ``(0,2)`` m_cx_2 = tqs.CycleMatch(cyc_cx_alt) m_entangling = m_past & (m_present | m_cx_2)
- Parameters:
lag (
int) – This instance will match to the cycle which occuredlagcycles in the past. By default, this is 0, and matches to the present cycle.exclusive (
bool) – Whether to mark every operation yielded during iteration asno_more_noise. In any future iterations by anyMatchan operation with this marking will be skipped.
- check_match(cycle_wrappers)
Abstract method to be overwritten by children which defines the cycle matching function. This function should return
Trueif the desired cycle withincycle_wrappersmatches the conditions of the match, andFalseotherwise.- Parameters:
cycle_wrappers (
list) – A list ofCycleWrappers to match against.
- property lag
Returns the number of cycles this match instance lags the present cycle by.
- Returns:
The number of cycles behind the current cycle being matched to.
- Type:
int
- find_matches(cycle_wrappers)
If the
cycle_wrappersmatch to this instance, this method returns this match object in a list, or an empty list otherwise. This instance’s matching function is given bycheck_match().- Parameters:
cycle_wrappers (
list) – A list ofCycleWrappers to match against.- Returns:
A list containing this match instance if the cycle matches, and an empty list otherwise.
- Return type:
list
- class trueq.simulation.match.AndCycleMatch(*matches, exclusive=None)
Instances of this class match operations that match the intersection of the given
matches. Allmatchesmust be children ofBaseCycleMatch. Operations are matched as follows:Any operation that matches all of the given
matches.However, any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
- Parameters:
*matches – One or more
BaseCycleMatches of any type.exclusive (
bool|NoneType) – Whether to mark every operation yielded during iteration asno_more_noise. In any future iterations by anyMatchan operation with this marking will be skipped.
- class trueq.simulation.match.AssociativeCycleMatch(*matches, exclusive=None)
Abstract parent class for children
Cthat stores a list ofBaseCycleMatches and have the property thatC([A, C([B, C]))andC([A, B, C])share the same behaviour. This flattening process is performed automatically by the constructor whenAssociativeCycleMatches of the same type are encountered.- Parameters:
*matches – One or more
BaseCycleMatches of any type.exclusive (
bool|NoneType) – Whether to mark every operation yielded during iteration asno_more_noise. In any future iterations by anyMatchan operation with this marking will be skipped.
- Raises:
ValueError – If any match in
matchesis not a child class ofBaseCycleMatch.
- class trueq.simulation.match.CycleMatch(cycle, ignore_marker=True, ignore_id=False, lag=0, exclusive=False)
Instances of this class match all operations in a given cycle equivalent to the cycle used to instantiate this instance. By default, cycle equivalence means cycle equality, but the boolean arguments
ignore_markerandignore_idallow three more variants of cycle equivalence. Operations are matched as follows:All operations in a cycle if the cycle is equivalent to one of
cycles.However, any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
Additionally, this match instance has the ability to match on previously simulated cycles, allowing for the possibility of non-Markovian noise sources. By initializing an instance of this match with
lag > 0, the instance will match on the cycle simulatedlagcycles ago. By default,lagis0and matches on the cycle currently being simulated. This match will not match untillagcycles have been simulated.- Parameters:
ignore_marker (
bool) – Whether to ignore the marker values of cycles. Default isTrue.ignore_id (
bool) – Whether to treat all identity gates as though they are not present. Default isFalse.lag (
int) – This instance will match to the cycle which occuredlagcycles in the past. By default, this is 0, and matches to the present cycle.exclusive (
bool) – Whether to mark every operation yielded during iteration asno_more_noise. In any future iterations by anyMatchan operation with this marking will be skipped.
- class trueq.simulation.match.OrCycleMatch(*matches, exclusive=None)
Instances of this class match operations that match the union of the given
matches. Allmatchesmust be children ofBaseCycleMatch. Operations are matched as follows:Any operation that matches any of the given
matches.However, any presented
OpWrapperwhereno_more_noiseisTrueis skipped.
- Parameters:
*matches – One or more
BaseCycleMatches of any type.exclusive (
bool|NoneType) – Whether to mark every operation yielded during iteration asno_more_noise. In any future iterations by anyMatchan operation with this marking will be skipped.
CycleWrapper
- class trueq.simulation.match.CycleWrapper(cycle)
Wraps a
Cycleinto a list ofOpWrappers, partitioning the cycle ops into three groups,Gatewhich contains all gates,Measwhich contains all measurements, andPrepwhich contains all state preparations in the cycle being propagated by the simulator. The wrapper also contains theCycleitself, as well as its dimension viadim.A
CycleWrappercan be asked to return all gates which have not yet been simulated viafinal_iter(), serving as a final catch during cycle propagation, and is utilized by the parent class of noise sources,NoiseSourceduring the call ofapply().- Parameters:
cycle (
Cycle) – The cycle being wrapped.
OpWrapper
- class trueq.simulation.match.OpWrapper(labels, op)
Wraps labels and an
Operationinto one small object. The wrapper keeps track of whether or not it has been simulated viahas_been_simulated, which is marked asTrueduring cycle propagation within a simulation by aNoiseSource'sMatchwhen it simulates the action of the operation on the state. Further, it keeps track of whether some noise source has indicated that no further noise should be applied viano_more_noise, and is primarily modified by setting theexclusivevariable defined in aMatchtoTrue.Two
OpWrappers are equal if and only if all four of their properties are equal. That is, the labels and operations must be equal, as well as the state of their flags,has_been_simulatedandno_more_noise.
