Download

Download this file as Jupyter notebook: keys.ipynb.

Keys: Storing and Filtering Metadata

True-Q™ uses objects called Keys to store metadata. Each Circuit and Estimate owns a key which can store multiple name/value pairs in a dictionary-like format. Keys are used by all built-in circuit generation methods, such as SRB, to disambiguate the circuits that they generate from independent circuits that might happen to be in the same circuit collection. These metadata are what allow the main fitter, fit(), to keep track of all protocol types, cycles of interest, twirling groups, measurement bases, and so on, to provide separate estimates in each relevant context.

Keys can be constructed manually by providing the constructor keyname/value pairs.

[2]:

import trueq as tq
import matplotlib.pyplot as plt
import numpy as np

tq.Key(name="my_name", phi=27.7, shapes=("circle", "square"))

[2]:

Key(name='my_name', phi=27.7, shapes=('circle', 'square'))

In the following example, we combine some basic diagnostic protocols, SRB and IRB, in the same circuit collection, and display all resulting circuit keys in the fancy table format provided by KeySet.

[3]:

# create a single circuit collection with simultaneous RB, and simultaneous interleaved
# randomized benchmarking on two different cycles. for demonstration purposes, we have
# lowered the number of randomizations per sequence length below what a typical
# experiment would use
circuits = tq.make_srb(range(5), [4, 12], n_circuits=4)

cycle_h = tq.Cycle({range(5): tq.Gate.h})
circuits += tq.make_irb(cycle_h, [4, 10], n_circuits=3)

cycle_x = tq.Cycle({range(5): tq.Gate.x})
circuits += tq.make_irb(cycle_x, [2, 10], n_circuits=3)

circuits.keys()

[3]:
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".
KeySet
List of all the keys in the KeySet
 protocol
The characterization protocol used to generate a circuit.
 cycles twirl
The twirling group used to generate a circuit.
 n_random_cycles
The number of independent random cycles in the circuit.
 compiled_pauli
The n-qubit Pauli operator that was compiled into the circuit immediately before measurement.
 measurement_basis
An n-qubit Pauli operator describing the change-of-basis gates added prior to measurement.
Key
Key:
  • compiled_pauli: YIXXZ
  • cycles: (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 4
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),) Cliffords on [0, 1, 2, 3, 4] 4 YIXXZ ZZZZZ
Key
Key:
  • compiled_pauli: YZZXZ
  • cycles: (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 4
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),) Cliffords on [0, 1, 2, 3, 4] 4 YZZXZ ZZZZZ
Key
Key:
  • compiled_pauli: ZYIYI
  • cycles: (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 4
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),) Cliffords on [0, 1, 2, 3, 4] 4 ZYIYI ZZZZZ
Key
Key:
  • compiled_pauli: IIXXI
  • cycles: (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 10
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),) Cliffords on [0, 1, 2, 3, 4] 10 IIXXI ZZZZZ
Key
Key:
  • compiled_pauli: YIYYI
  • cycles: (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 10
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),) Cliffords on [0, 1, 2, 3, 4] 10 YIYYI ZZZZZ
Key
Key:
  • compiled_pauli: ZZZXZ
  • cycles: (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 10
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),) Cliffords on [0, 1, 2, 3, 4] 10 ZZZXZ ZZZZZ
Key
Key:
  • compiled_pauli: IYZYI
  • cycles: (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 2
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),) Cliffords on [0, 1, 2, 3, 4] 2 IYZYI ZZZZZ
Key
Key:
  • compiled_pauli: ZXIZZ
  • cycles: (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 2
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),) Cliffords on [0, 1, 2, 3, 4] 2 ZXIZZ ZZZZZ
Key
Key:
  • compiled_pauli: XZIZY
  • cycles: (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 2
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),) Cliffords on [0, 1, 2, 3, 4] 2 XZIZY ZZZZZ
Key
Key:
  • compiled_pauli: YIXIX
  • cycles: (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 10
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),) Cliffords on [0, 1, 2, 3, 4] 10 YIXIX ZZZZZ
Key
Key:
  • compiled_pauli: XYZXX
  • cycles: (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 10
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),) Cliffords on [0, 1, 2, 3, 4] 10 XYZXX ZZZZZ
Key
Key:
  • compiled_pauli: XIZXI
  • cycles: (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 10
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.x, (1,): Gate.x, (2,): Gate.x, (3,): Gate.x, (4,): Gate.x),) Cliffords on [0, 1, 2, 3, 4] 10 XIZXI ZZZZZ
Key
Key:
  • compiled_pauli: YXIYX
  • measurement_basis: ZZZZZ
  • n_random_cycles: 4
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 SRB Cliffords on [0, 1, 2, 3, 4] 4 YXIYX ZZZZZ
Key
Key:
  • compiled_pauli: XIYZI
  • measurement_basis: ZZZZZ
  • n_random_cycles: 4
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 SRB Cliffords on [0, 1, 2, 3, 4] 4 XIYZI ZZZZZ
Key
Key:
  • compiled_pauli: IZXZY
  • measurement_basis: ZZZZZ
  • n_random_cycles: 4
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 SRB Cliffords on [0, 1, 2, 3, 4] 4 IZXZY ZZZZZ
Key
Key:
  • compiled_pauli: YZYII
  • measurement_basis: ZZZZZ
  • n_random_cycles: 4
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 SRB Cliffords on [0, 1, 2, 3, 4] 4 YZYII ZZZZZ
Key
Key:
  • compiled_pauli: IZXZY
  • measurement_basis: ZZZZZ
  • n_random_cycles: 12
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 SRB Cliffords on [0, 1, 2, 3, 4] 12 IZXZY ZZZZZ
Key
Key:
  • compiled_pauli: XZIXI
  • measurement_basis: ZZZZZ
  • n_random_cycles: 12
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 SRB Cliffords on [0, 1, 2, 3, 4] 12 XZIXI ZZZZZ
Key
Key:
  • compiled_pauli: ZIZYY
  • measurement_basis: ZZZZZ
  • n_random_cycles: 12
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 SRB Cliffords on [0, 1, 2, 3, 4] 12 ZIZYY ZZZZZ
Key
Key:
  • compiled_pauli: ZYXIZ
  • measurement_basis: ZZZZZ
  • n_random_cycles: 12
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 SRB Cliffords on [0, 1, 2, 3, 4] 12 ZYXIZ ZZZZZ

We can look at the key of a particular circuit, inspect its values either with property syntax, or subscript syntax, and perform other container-like actions.

[4]:

# get the whole key
circuits[0].key

[4]:

Key(compiled_pauli=Weyls('YZYII'), measurement_basis=Weyls('ZZZZZ'), n_random_cycles=4, protocol='SRB', twirl=Twirl({(0,): 'C', (1,): 'C', (2,): 'C', (3,): 'C', (4,): 'C'}, dim=2))

[5]:

# get all keywords (names) present in the key
circuits[0].key.names

[5]:

('compiled_pauli', 'measurement_basis', 'n_random_cycles', 'protocol', 'twirl')

[6]:

# find out whether the key contains a particular keyword (name)
"protocol" in circuits[0].key

[6]:

True

[7]:

# inspect a particular value using property syntax
circuits[0].key.compiled_pauli

[7]:
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".
Type:
  • Weyls
Dim:
  • 2
Powers:
X0 X1 X2 X3 X4 Z0 Z1 Z2 Z3 Z4
0 1 0 1 0 0 1 1 1 0 0 
[8]:

# inspect a particular value using subscript syntax
circuits[0].key["measurement_basis"]

[8]:
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".
Type:
  • Weyls
Dim:
  • 2
Powers:
X0 X1 X2 X3 X4 Z0 Z1 Z2 Z3 Z4
0 0 0 0 0 0 1 1 1 1 1

If we have a KeySet, as returned by keys(), we can look at all unique values associated with a particular keyword to quickly identify the contents of a collection.

[9]:

# our collection contains circuits generated by the SRB and IRB protocols
circuits.keys().protocol

[9]:

{'IRB', 'SRB'}

[10]:

# all circuits present use simultaneous single-qubit Clifford twirling
circuits.keys().twirl

[10]:

{Twirl({(0,): 'C', (1,): 'C', (2,): 'C', (3,): 'C', (4,): 'C'}, dim=2)}

Filtering Based on Keys

Keys are designed to allow fast filtering of large collections. Circuit and estimate collections contain the respective methods subset() and subset() for this purpose. We use the circuit collection created in the previous subsection, though the mechanics of filtering estimate collections are identical.

There are three ways that circuits can be filtered based on key values, (which can all be used together on different keywords in the same filtering operation):

  1. By exact value equality.

[11]:

# collect all SRB circuits into a new collection
srb_circuits = circuits.subset(protocol="SRB")

  1. By value containment in some allowed set of values.

[12]:

# collect all circuits with sequence length 2 or 4. the use of a set is necessary
short_circuits = circuits.subset(n_random_cycles={2, 4})

  1. By value exclusion from some list of disallowed values.

[13]:

# collect all circuits whose sequence length is not 2 or 4. the use of list is necessary
long_circuits = circuits.subset(n_random_cycles=[2, 4])

We can combine the three types of filtering in a single operation, as seen below.

[14]:

irb_circuits_h = circuits.subset(cycles=(cycle_h,), n_random_cycles={2, 4})
irb_circuits_h.keys()

[14]:
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".
KeySet
List of all the keys in the KeySet
 protocol
The characterization protocol used to generate a circuit.
 cycles twirl
The twirling group used to generate a circuit.
 n_random_cycles
The number of independent random cycles in the circuit.
 compiled_pauli
The n-qubit Pauli operator that was compiled into the circuit immediately before measurement.
 measurement_basis
An n-qubit Pauli operator describing the change-of-basis gates added prior to measurement.
Key
Key:
  • compiled_pauli: YIXXZ
  • cycles: (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 4
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),) Cliffords on [0, 1, 2, 3, 4] 4 YIXXZ ZZZZZ
Key
Key:
  • compiled_pauli: YZZXZ
  • cycles: (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 4
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),) Cliffords on [0, 1, 2, 3, 4] 4 YZZXZ ZZZZZ
Key
Key:
  • compiled_pauli: ZYIYI
  • cycles: (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),)
  • measurement_basis: ZZZZZ
  • n_random_cycles: 4
  • protocol: IRB
  • twirl: Cliffords on [0, 1, 2, 3, 4]
 IRB (Cycle((0,): Gate.h, (1,): Gate.h, (2,): Gate.h, (3,): Gate.h, (4,): Gate.h),) Cliffords on [0, 1, 2, 3, 4] 4 ZYIYI ZZZZZ

Using Keys in Custom Circuits

Users are encouraged to use keys to attach metadata to their own circuits. In the following demonstration, we create a collection of circuits which produce a 5 qubit GHZ state, rotate each qubit about Z by some angle phi, and then undo the GHZ state to measure the total phase accumulation. We use the key to keep track of which phase each circuit contains.

[15]:

circuits = tq.CircuitCollection()
for phi in np.linspace(-180, 180, 61):
    circuit = tq.Circuit(key=tq.Key(phi=phi, measurement_basis=tq.math.Weyls("Z")))
    circuit += {0: tq.Gate.h}
    circuit += [{(i, i + 1): tq.Gate.cx} for i in range(4)]
    circuit += {range(5): tq.Gate.rz(phi)}
    circuit += [{(i, i + 1): tq.Gate.cx} for i in reversed(range(4))]
    circuit += [{0: tq.Gate.h}, {0: tq.Meas()}]

    circuits += circuit

# draw an example circuit
circuits[5].draw(False)

[15]:
0 1 2 3 4 H CX CX CX CX CX CX CX CX CX CX CX CX CX CX CX CX H M

Next, we attach results to all circuits in the collection with a noisy simulator.

[16]:

sim = tq.Simulator().add_overrotation(0.04, 0.08).add_stochastic_pauli(px=0.01)
sim.run(circuits, n_shots=128)

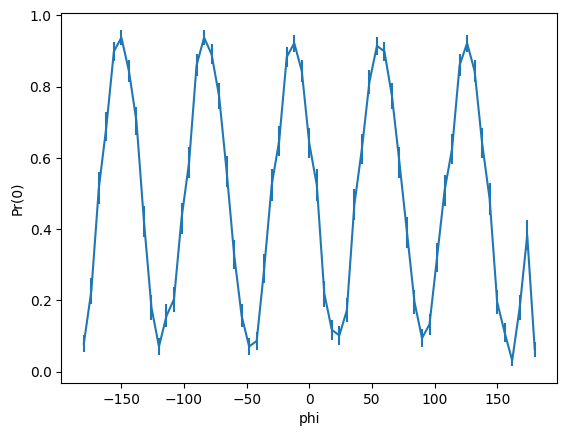
Finally, we can extract values from each circuit’s results and key to produce a plot.

[17]:

xs, ys = [], []
for circuit in circuits:
    xs.append(circuit.key.phi)
    ys.append(circuit.results[0] / 128)
ys = np.array(ys)
plt.errorbar(xs, ys, yerr=np.sqrt(ys * (1 - ys) / 128))
plt.xlabel("phi")
plt.ylabel("Pr(0)")

[17]:

Text(0, 0.5, 'Pr(0)')
../../_images/guides_fundamentals_keys_27_1.png

Augmenting True-Q™ Generated Circuits with User Metadata

We also encourage users to augment key metadata generated by True-Q™ protocols with their own keynames/values when convenient. In the following example, we insert SRB circuits into a circuit collection 11 times, each time augmenting the new circuits with an additional keyname eps whose value records how much single-qubit overrotation noise we have included in their simulation.

[18]:

circuits = tq.CircuitCollection()
for eps in np.linspace(0, 0.05, 11):
    srb_circuits = tq.make_srb(range(3), [4, 12, 24, 48]).update_keys(eps=eps)
    tq.Simulator().add_overrotation(eps).run(srb_circuits)
    circuits += srb_circuits

Importantly, the fitter will treat these 11 groups independently, so that in the following table we see estimates for each of the three qubits, and for each of the 11 values of eps. Hovering over a cell in the top row of the table will produce a tooltip containing the full contents of the respective estimate’s key.

[19]:

fit = circuits.fit()
fit

[19]:
True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".
SRB
Streamlined Randomized Benchmarking
 Cliffords
(0,)
Key:
  • eps: 0.01
  • labels: (0,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(0,)
Key:
  • eps: 0.015
  • labels: (0,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(0,)
Key:
  • eps: 0.02
  • labels: (0,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(0,)
Key:
  • eps: 0.05
  • labels: (0,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(0,)
Key:
  • eps: 0.025
  • labels: (0,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(0,)
Key:
  • eps: 0.005
  • labels: (0,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(0,)
Key:
  • eps: 0.03
  • labels: (0,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(0,)
Key:
  • eps: 0.035
  • labels: (0,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(0,)
Key:
  • eps: 0.0
  • labels: (0,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(0,)
Key:
  • eps: 0.045
  • labels: (0,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(0,)
Key:
  • eps: 0.04
  • labels: (0,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(1,)
Key:
  • eps: 0.0
  • labels: (1,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(1,)
Key:
  • eps: 0.025
  • labels: (1,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(1,)
Key:
  • eps: 0.03
  • labels: (1,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(1,)
Key:
  • eps: 0.04
  • labels: (1,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(1,)
Key:
  • eps: 0.01
  • labels: (1,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(1,)
Key:
  • eps: 0.02
  • labels: (1,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(1,)
Key:
  • eps: 0.05
  • labels: (1,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(1,)
Key:
  • eps: 0.045
  • labels: (1,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(1,)
Key:
  • eps: 0.035
  • labels: (1,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(1,)
Key:
  • eps: 0.005
  • labels: (1,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(1,)
Key:
  • eps: 0.015
  • labels: (1,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(2,)
Key:
  • eps: 0.015
  • labels: (2,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(2,)
Key:
  • eps: 0.05
  • labels: (2,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(2,)
Key:
  • eps: 0.025
  • labels: (2,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(2,)
Key:
  • eps: 0.035
  • labels: (2,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(2,)
Key:
  • eps: 0.04
  • labels: (2,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(2,)
Key:
  • eps: 0.01
  • labels: (2,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(2,)
Key:
  • eps: 0.045
  • labels: (2,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(2,)
Key:
  • eps: 0.02
  • labels: (2,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(2,)
Key:
  • eps: 0.03
  • labels: (2,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(2,)
Key:
  • eps: 0.0
  • labels: (2,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
 Cliffords
(2,)
Key:
  • eps: 0.005
  • labels: (2,)
  • protocol: SRB
  • twirl: Cliffords on [0, 1, 2]
${e}_{F}$
The probability of an error acting on the targeted systems during a random gate.
1.9e-04 (7.6e-05)
0.00019353979412831124, 7.61063417464499e-05
 2.9e-04 (1.1e-04)
0.0002896341197081709, 0.00010954768695538254
 7.2e-04 (1.9e-04)
0.0007198286713262225, 0.0001947932536710911
 3.1e-03 (7.1e-04)
0.003082796054407533, 0.0007129215831005582
 1.2e-03 (3.1e-04)
0.0012189456867393866, 0.00031481406800917643
 0.0e+00 (0.0e+00)
0.0, 0.0
 9.5e-04 (2.7e-04)
0.000949474612108786, 0.00026788998152784023
 1.7e-03 (4.7e-04)
0.0017278178859618798, 0.0004728237017700579
 0.0e+00 (0.0e+00)
0.0, 0.0
 3.4e-03 (6.2e-04)
0.0034083790600174524, 0.0006182355859500265
 4.4e-03 (8.7e-04)
0.004430998232375721, 0.0008661334470995615
 0.0e+00 (0.0e+00)
0.0, 0.0
 9.9e-04 (2.3e-04)
0.0009906192927170154, 0.00022781773929199568
 1.5e-03 (3.4e-04)
0.0015374715695321839, 0.00033516622380352576
 2.4e-03 (4.6e-04)
0.002423894069629451, 0.0004640629160270162
 7.6e-05 (5.6e-05)
7.641316533166242e-05, 5.5625556206341865e-05
 8.3e-04 (2.4e-04)
0.0008316746243000883, 0.0002378839071263226
 3.8e-03 (1.1e-03)
0.003816370715785139, 0.001113194343734625
 3.2e-03 (8.1e-04)
0.003232897915771943, 0.0008137882725766788
 2.2e-03 (6.3e-04)
0.0022344508246257277, 0.0006261649399067292
 0.0e+00 (0.0e+00)
0.0, 0.0
 4.1e-04 (1.4e-04)
0.0004077645758473192, 0.00014339938349891622
 3.6e-04 (1.6e-04)
0.00036233417503653276, 0.00015746551990921624
 3.3e-03 (7.2e-04)
0.0032862289331225536, 0.0007160607889887767
 1.0e-03 (3.3e-04)
0.0009979323777910276, 0.00032502171619740346
 3.4e-03 (8.2e-04)
0.003381545115102358, 0.0008229864402108287
 2.3e-03 (5.7e-04)
0.0023038973914002725, 0.0005676796583645643
 8.0e-05 (8.1e-05)
8.005537718502875e-05, 8.071638044706117e-05
 4.1e-03 (1.2e-03)
0.004082804558789871, 0.0012081031717783343
 7.1e-04 (2.1e-04)
0.0007135241462784547, 0.00020958629795477174
 1.1e-03 (2.4e-04)
0.001057397700929552, 0.00024387987636440356
 0.0e+00 (0.0e+00)
0.0, 0.0
 1.1e-04 (5.0e-05)
0.00011088847819398784, 5.007681532564742e-05
${p}$
Decay parameter of the exponential decay $Ap^m$.
1.0e+00 (1.0e-04)
0.9997419469411623, 0.00010147512232859987
 1.0e+00 (1.5e-04)
0.9996138211737224, 0.0001460635826071767
 1.0e+00 (2.6e-04)
0.9990402284382317, 0.0002597243382281214
 1.0e+00 (9.5e-04)
0.99588960526079, 0.0009505621108007444
 1.0e+00 (4.2e-04)
0.9983747390843475, 0.0004197520906789019
 1.0e+00 (0.0e+00)
1.0, 0.0
 1.0e+00 (3.6e-04)
0.9987340338505216, 0.0003571866420371203
 1.0e+00 (6.3e-04)
0.9976962428187175, 0.0006304316023600772
 1.0e+00 (0.0e+00)
1.0, 0.0
 1.0e+00 (8.2e-04)
0.9954554945866434, 0.0008243141146000353
 9.9e-01 (1.2e-03)
0.9940920023568324, 0.0011548445961327488
 1.0e+00 (0.0e+00)
1.0, 0.0
 1.0e+00 (3.0e-04)
0.9986791742763773, 0.0003037569857226609
 1.0e+00 (4.5e-04)
0.9979500379072904, 0.000446888298404701
 1.0e+00 (6.2e-04)
0.9967681412404941, 0.0006187505547026882
 1.0e+00 (7.4e-05)
0.9998981157795578, 7.416740827512249e-05
 1.0e+00 (3.2e-04)
0.9988911005009332, 0.0003171785428350968
 9.9e-01 (1.5e-03)
0.9949115057122865, 0.0014842591249795
 1.0e+00 (1.1e-03)
0.9956894694456374, 0.0010850510301022383
 1.0e+00 (8.3e-04)
0.9970207322338324, 0.0008348865865423055
 1.0e+00 (0.0e+00)
1.0, 0.0
 1.0e+00 (1.9e-04)
0.9994563138988702, 0.00019119917799855494
 1.0e+00 (2.1e-04)
0.999516887766618, 0.00020995402654562165
 1.0e+00 (9.5e-04)
0.9956183614225033, 0.0009547477186517021
 1.0e+00 (4.3e-04)
0.9986694234962786, 0.0004333622882632046
 1.0e+00 (1.1e-03)
0.9954912731798635, 0.0010973152536144382
 1.0e+00 (7.6e-04)
0.9969281368114663, 0.0007569062111527524
 1.0e+00 (1.1e-04)
0.9998932594970866, 0.00010762184059608157
 9.9e-01 (1.6e-03)
0.9945562605882802, 0.0016108042290377792
 1.0e+00 (2.8e-04)
0.9990486344716287, 0.000279448397273029
 1.0e+00 (3.3e-04)
0.9985901363987606, 0.0003251731684858714
 1.0e+00 (0.0e+00)
1.0, 0.0
 1.0e+00 (6.7e-05)
0.9998521486957413, 6.676908710086324e-05
${A}$
SPAM parameter of the exponential decay $Ap^m$.
1.0e+00 (1.9e-03)
0.9996501901807677, 0.001853245349922514
 1.0e+00 (2.7e-03)
0.999770666810547, 0.0026743150084148695
 1.0e+00 (4.5e-03)
0.9973591319109976, 0.004492032632454417
 9.7e-01 (1.7e-02)
0.9707063342337384, 0.016830682230242713
 1.0e+00 (5.6e-03)
1.0046280328654755, 0.005608449836532985
 1.0e+00 (0.0e+00)
1.0, 0.0
 9.9e-01 (5.8e-03)
0.9903202883380763, 0.00575314153306841
 9.8e-01 (1.0e-02)
0.9811014203979889, 0.01020893193519766
 1.0e+00 (0.0e+00)
1.0, 0.0
 9.8e-01 (1.4e-02)
0.9784199417450851, 0.01370169534395814
 1.0e+00 (1.5e-02)
1.0248239536382793, 0.015385220978427702
 1.0e+00 (0.0e+00)
1.0, 0.0
 1.0e+00 (5.2e-03)
0.9976847778354518, 0.0051533560456752305
 1.0e+00 (6.7e-03)
1.005145472522628, 0.006729950340969296
 9.9e-01 (9.3e-03)
0.9910039945137397, 0.009346342341513882
 1.0e+00 (1.7e-03)
0.9989008077030794, 0.001746273995019393
 1.0e+00 (4.2e-03)
1.0036974142390553, 0.004196923061056229
 1.0e+00 (1.9e-02)
1.005930426904904, 0.018854284077089018
 9.8e-01 (1.5e-02)
0.9831921707057751, 0.01458873950828973
 9.8e-01 (1.3e-02)
0.9822176256548445, 0.013424800167979749
 1.0e+00 (0.0e+00)
1.0, 0.0
 1.0e+00 (2.8e-03)
1.0005256002289462, 0.002830906955117178
 1.0e+00 (3.1e-03)
0.9995343629931396, 0.003108591956647165
 1.0e+00 (1.3e-02)
1.0000358405994731, 0.013216905359532129
 1.0e+00 (6.3e-03)
0.9978659935074863, 0.006342458870360639
 1.0e+00 (1.4e-02)
1.00709571930024, 0.014429516671272891
 1.0e+00 (1.0e-02)
1.0027454380498435, 0.010034200899936473
 1.0e+00 (1.8e-03)
0.9990079916988585, 0.001773949369872166
 1.0e+00 (2.1e-02)
0.9971370094009, 0.021232648956257653
 1.0e+00 (4.1e-03)
0.9999296912187626, 0.004090961050026459
 9.9e-01 (6.8e-03)
0.9868885399628784, 0.006764615761543387
 1.0e+00 (0.0e+00)
1.0, 0.0
 1.0e+00 (1.0e-03)
1.0009140281025375, 0.0009993057434390642
 
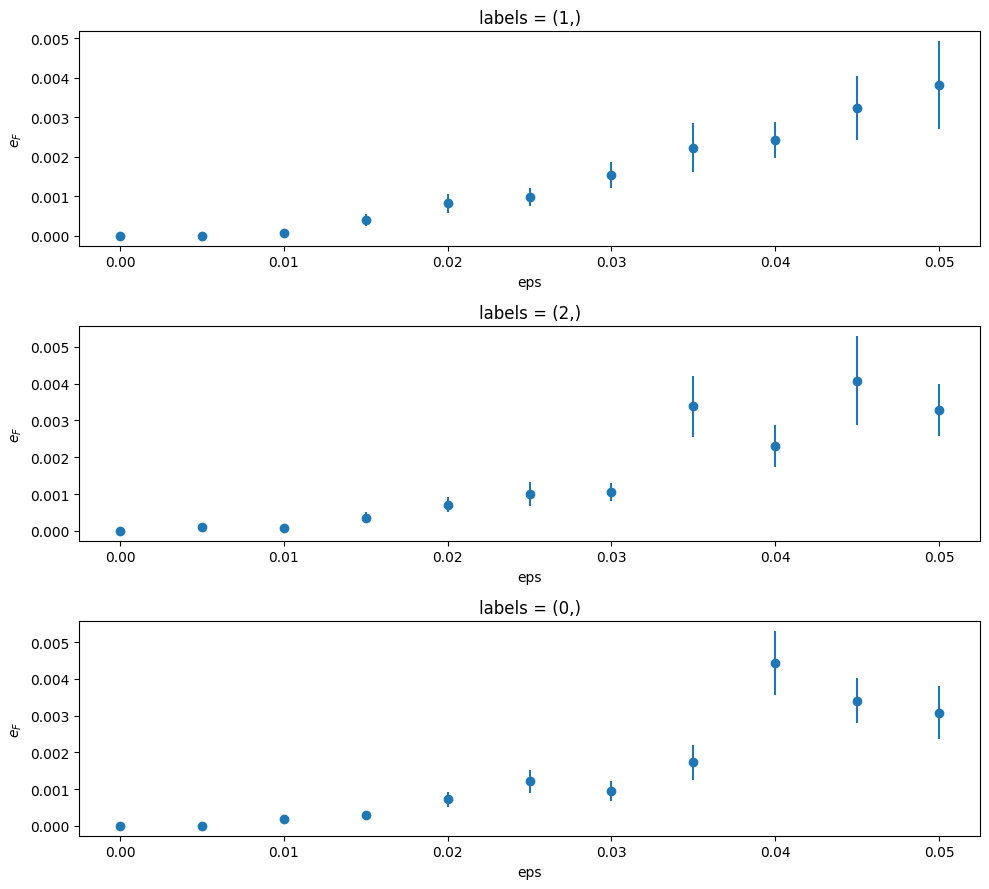
[20]:

fit.plot.compare("e_F", "eps")
../../_images/guides_fundamentals_keys_32_0.png

Special Keywords

True-Q™ uses the following keywords for Keys internally. There are no restrictions on using these keywords for your own purposes, or manually overriding them, but doing so may cause fitting and other features to break.

Keyword

Description

amplification

Used by NOX to specify noise amplification.

analyze_decays

Stores CB decays to measure.

batch

Used by RCAL to index experiment batches.

compiled_pauli

Which Paulis were compiled prior to measurements.

cycles

The cycles of interest, see e.g. CB.

labels

A tuple of qubit labels.

measurement_basis

Which basis change was compiled into the circuit.

mitigation

The name of a mitigation protocol, e.g. NOX.

n_random_cycles

The number of independent random cycles in a circuit.

order

Sometimes used to order by key.

protocol

The name of a protocol, e.g. CB.

relabeling

Stores how a circuit was relabeled by a compiler.

seq_label

Used to index small variations of a common random circuit.

subsystems

Used by KNR to specify the gate-bodies to probe.

targeted_errors

Non-identity errors targeted by CB.

twirl

Stores the twirling group.

Usually, fit() produces a separate set of estimates for every unique combination of custom keywords (i.e. not in the list above). The exceptions to this rule are the following custom keywords, which will be ignored and deleted in the returned fit object:

Keyword

Description

job_id

E.g. store a job execution identifier.

n_shots

E.g. store a recommended number of shots for a circuit.

Download

Download this file as Jupyter notebook: keys.ipynb.