Selecting Parameters for Error Diagnostics (Advanced)

The introductory Selecting Parameters for Error Diagnostics tutorial covers the basic needs of True-Q™’s error diagnostics protocols. Here we will explore some of the more advanced customization options for these methods. The table below shows which of True-Q™’s error diagnostic protocols use which arguments.

Arguments for Error Diagnostic Protocols

	cycles	n_random_cycles	n_circuits	n_decays	twirl	propagate_correction	compiled_pauli	labels	Special Arguments
Cycle Benchmarking (CB)	X	X	X	X	X	X	X		targeted_errors
Crosstalk Diagnostics (CTD)		X	X					X	subsets, include_xrb
Interleaved Randomized Benchmarking (IRB)	X	X	X		X	X	X
K-body Noise Reconstruction (KNR)	X	X	X		X	X	X		subsystems
Streamlined Randomized Benchmarking (SRB)		X	X				X	X
Extended Randomized Benchmarking (XRB)		X	X					X
Quantum Capacity (QCAP)	X	X	X	X

The n_random_cycles and n_circuits arguments

These two parameters are used by every diagnostic protocol and are covered in Selecting Parameters for Error Diagnostics.

The cycles argument

Many of True-Q™’s error diagnostic protocols characterize the noise that arises as a result of implementing a specific Cycle. For these protocols, cycles tells the protocol which cycle to characterize.

The n_decays argument

The n_decays argument specifies the number of randomly sampled Paulis for which a protocol will estimate the expectation value. These expectation values will then be used to approximate the parameter of interest. Increasing n_decays improves the accuracy of the estimated parameter, but also increases the overhead of the protocol.

Note

Setting n_decays lower than:

1. \(\textrm{min}(20, 4\: \times\) n_qubits \(- 1)\) may result in a biased estimate of the process fidelity.

2. \(\textrm{min}(40, 4\: \times\) n_qubits \(- 1)\) may result in a biased estimate of the probability of non-identity errors.

The twirl argument

The twirl argument accepts a Twirl object to tell a diagnostic (or suppression) protocol which twirling group to select random gates from when constructing circuits to average over. For some protocols, the twirling group is implicit or irrelevant to the protocol and therefore this argument only pertains to a subset of True-Q™’s protocols and is always an optional argument. Below, we give a breakdown of which protocols use which twirling groups by default and which are customizable.

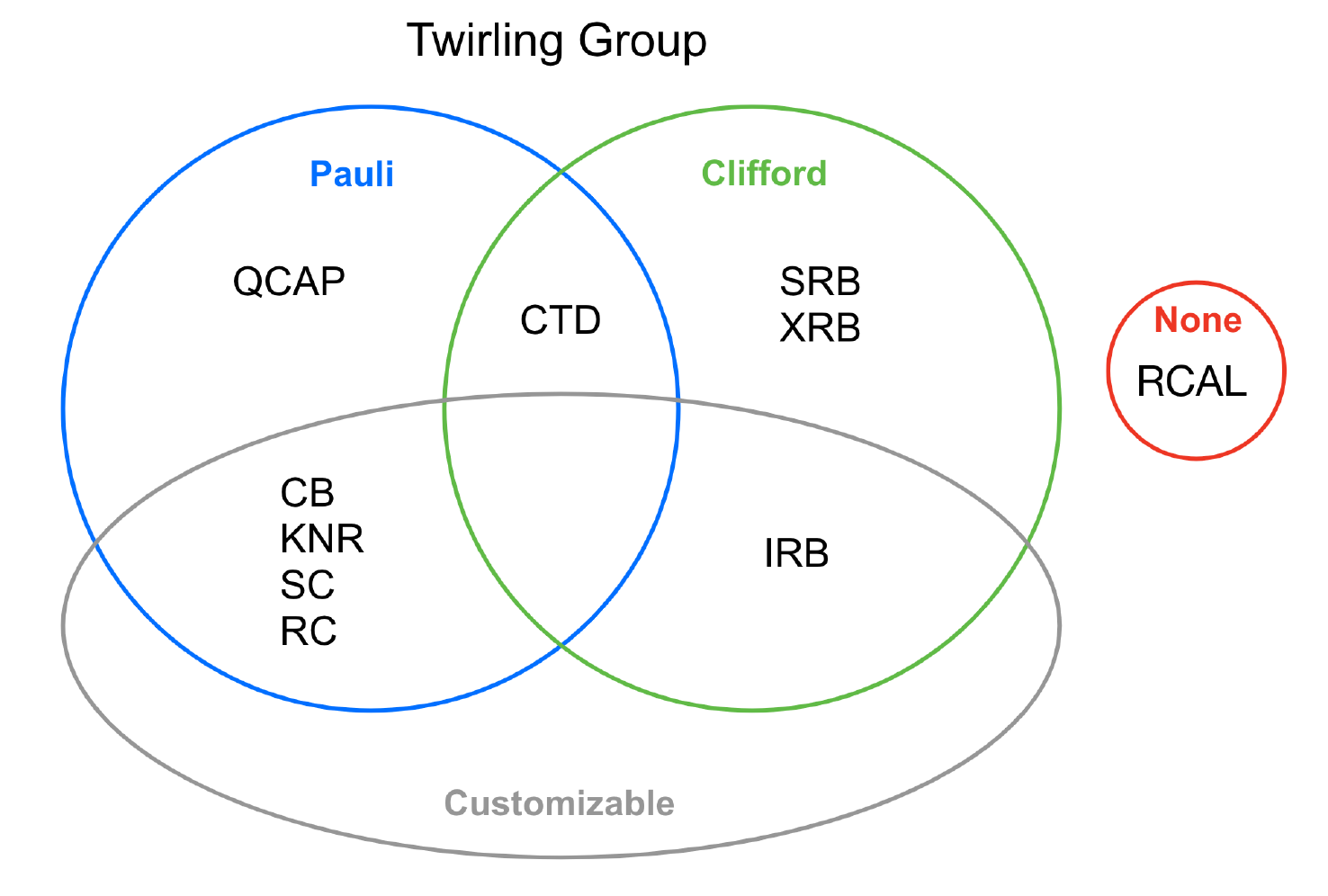
Twirling with respect to the Pauli group projects a channel onto the Pauli basis, that is, removes the non-Pauli part of the noise. Twirling with respect to the Clifford group results in a depolarizing channel, that is a Pauli channel for which the probability of error is equal for any of the Pauli errors. For this reason, the error diagnostic protocols which return a single parameter of interest in the form of an average fidelity for the twirling group generally use the Clifford group, since twirling by the Clifford group makes the effects from different group elements uniform. By the same reasoning, error diagnostic protocols which are designed to isolate the effects or probabilities of specific errors typically use the Pauli group.

Another common reason to define a custom twirl is to include idling qubits in the analysis, as shown in Example: Running KNR.

The propagate_correction argument

Some error diagnostic protocols compile gates into the circuit with the aim of replicating a given effective operation despite the addition of random gates. In these protocols, additional correction gates are compiled into the circuit to offset the random gates to ensure that the net effect of the compilation preserves the desired operation. The propagate_correction argument tells True-Q™ whether to propagate these additional correction gates to the end of the circuit rather than compiling them into neighbouring cycles. propagate_correction is set to False by default.

The compiled_pauli argument

The compiled_pauli argument allows users to customize a change of basis that happens right before measurement. This argument accepts either a string of Paulis to compile onto each qubit in the cycle preceding a measurement operation or a boolean value, which tells True-Q™ whether to compile a random Pauli gate onto each qubit in the cycle preceding measurement. Applying random Pauli operators to a CircuitCollection before measurement effectively applies a Pauli twirl to any noise on the measurement operations. This has the effect of stabilizing the statistics of the diagnostic protocols, and thereby improves the accuracy of the parameter estimates. For this reason, compiled_pauli is set to True by default.

The Paulis that are compiled into the cycle before the measurement are accounted for when results are fitted. That is, if a Pauli is compiled in before the measurement which will change the outcome of the measurement, the fitting function for the diagnostic tool being applied will modify the fitting to offset the change.

The labels argument

Protocols which do not characterize a specific cycle, but instead an empty cycle or readout take labels as an argument to tell the protocol which subsystems to target. That is, if you want to target the qubit labeled 0, set labels = 0. To characterize noise on qubits 0 and 1 independently, set labels = [0, 1]. If you want to characterize the joint pair containing qubits 0 and 1, and qubit 2 independently, you would set labels = [[0, 1], 2].