Download

Download this file as Jupyter notebook: nox_example.ipynb.

Example: Running Noiseless Output Extrapolation

This example illustrates how to generate noiseless output extrapolation (NOX) circuits and use them to obtain error-mitigated outputs from noisy simulations.

NOX on Qubits

First, we initialize a noisy simulator with depolarizing noise on $CX$ gates and with readout errors.

[2]:

import trueq as tq
import trueq.simulation as tqs

# make a noisy simulator
sim = tq.Simulator().add_depolarizing(0.03, match=tqs.GateMatch(tq.Gate.cx))
sim.add_readout_error(0.01)

[2]:

<trueq.simulation.simulator.Simulator at 0x7f57d8d9eb50>

We are going to use NOX to mitigate these cycles’ errors in a circuit that generates a five-qubit Greenberger–Horne–Zeilinger (GHZ) state. We begin by creating our circuit.

[3]:

# create the circuit
circuit = tq.Circuit(
    [
        {0: tq.Gate.h},
        {(0, 1): tq.Gate.cx},
        {(0, 2): tq.Gate.cx, (1, 3): tq.Gate.cx},
        {(0, 4): tq.Gate.cx},
    ]
).measure_all()

# show the circuit
circuit.draw()

[3]:

Using the make_nox() function, we generate circuits to amplify the noise in each hard cycle of the circuit.

Note

When it comes to the optional parameters for make_nox(), increasing n_identities can reduce the standard deviation of the estimates, provided that the error on the deeper circuit is not too large. Applying several random compilations to each circuit transforms the noise processes into Pauli channels which is recommended for NOX. We generally expect n_compilations between 15 and 30 to be sufficient.

The circuit shown below amplifies the noise on the first hard cycle, which contains a $CX$ gate acting on qubits (0, 1).

[4]:

# generate the NOX circuits
nox_circuits = tq.make_nox(circuit, n_identities=2, n_compilations=30)

# show the circuit which amplifies noise on the first hard cycle
nox_circuits[1].draw()

[4]:

We now run the circuits on our noisy simulator. We analyze and fit the results by calling the fit() method. This method automatically uses the results of the NOX circuits to improve the estimate of user-specified observables and outcomes. The table shows an estimate of the expected value of each observable and outcome, and its standard deviation.

[5]:

# run the simulation
sim.run(nox_circuits, n_shots=500)

# set which observables and outcomes to estimate
labels = ((0, 1, 2, 3),)
observables = ["0000", "1111", "ZIZI"]

# fit
fit = nox_circuits.fit(labels, observables=observables)
fit

[5]:

True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".

NOX Noiseless Output Extrapolation	Circuit #0 Labels (0, 1, 2, 3) Key: labels: (0, 1, 2, 3) measurement_basis: ZZZZ mitigation: ('NOX',) n_marked: 3 protocol: RC seq_label: 202885529 twirl: Paulis on [0, 1, 2, 3, 4]
$ev_\texttt{ZIZI}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	9.8e-01 (7.1e-03) 0.9810333333333333, 0.007115869157715681
$ev_\texttt{1111}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	4.8e-01 (8.5e-03) 0.4835166666666666, 0.00848831121030946
$ev_\texttt{0000}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	4.7e-01 (6.8e-03) 0.4740000000000001, 0.006756478372643374

We can plot the estimates from each NOX circuit alongside the mitigated estimates. The point farthest to the left shows the unmitigated estimate. The subsequent points correspond to the estimates for each circuit with one cycle having amplified noise. Finally, the mitigated estimate is on the right.

[6]:

# plot the results for the ZZZZ observable
fit.plot.raw_nox(observables=["0000"])

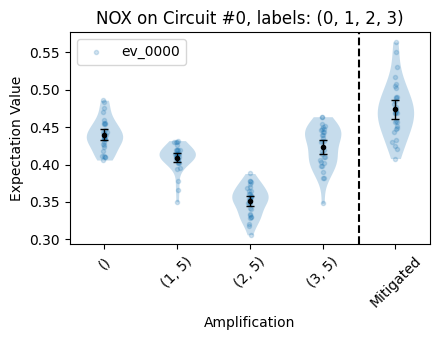
../../_images/guides_error_suppression_nox_example_10_0.png

We can see the benefits of using NOX by comparing the NOX-mitigated results and the unmitigated results. To retrieve the results from the unmitigated circuits, we select the subset of NOX circuits with no noise amplification. As shown below, the estimated expectation values of the outputs 00000 and 11111 are closer to the correct values for the NOX circuits than for the unmitigated circuits.

[7]:

# unmitigated results
sim.run(circuit, n_shots=15000)
res_unmit = circuit.get_probability(["00000", "11111"])

# nox results
res_nox = nox_circuits.fit(observables=["00000", "11111"]).array("ev_\d*").vals

print("Prob. of output 00000")
print("Correct value: 0.50")
print(f"Unmitigated circuits: {res_unmit[0]:.2f}")
print(f"Mitigated circuits: {res_nox[0]:.2f}")

print("\nProb. of output 11111")
print("Correct value: 0.50")
print(f"Unmitigated circuits: {res_unmit[1]:.2f}")
print(f"Mitigated circuits: {res_nox[1]:.2f}")

Prob. of output 00000
Correct value: 0.50
Unmitigated circuits: 0.43
Mitigated circuits: 0.47

Prob. of output 11111
Correct value: 0.50
Unmitigated circuits: 0.43
Mitigated circuits: 0.48

NOX with RCAL

NOX can be used in tandem with readout calibration (RCAL) to achieve even better results. The noisy simulator we created above suffers from readout errors. To correct these errors, we run RCAL circuits. As we see below, if the NOX circuit collection also contains RCAL circuits, readout errors will automatically be mitigated when we call the fit() method.

[8]:

# create and run RCAL circuits
rcal_circuits = tq.make_rcal([0, 1, 2, 3, 4])
sim.run(rcal_circuits, n_shots=5000)

# add RCAL circuits to circuit collection
nox_circuits.append(rcal_circuits)

# get the results
# the readout calibration correction is automatically applied when we fit
fit = nox_circuits.fit(observables=["00000", "11111", "01100", "ZZIIZ"])
fit

[8]:

True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".

NOX Noiseless Output Extrapolation	Circuit #0 Labels (0, 1, 2, 3, 4) Key: labels: (0, 1, 2, 3, 4) measurement_basis: ZZZZZ mitigation: ('NOX',) n_marked: 3 protocol: RC seq_label: 202885529 twirl: Paulis on [0, 1, 2, 3, 4]
$ev_\texttt{ZZIIZ}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	-1.3e-02 (1.6e-02) -0.013067925890280432, 0.016302214404336355
$ev_\texttt{11111}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	5.1e-01 (8.7e-03) 0.5051758270964705, 0.008675205683536146
$ev_\texttt{01100}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	-9.3e-05 (3.8e-04) -9.2566788905739e-05, 0.0003837676511486187
$ev_\texttt{00000}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	4.9e-01 (7.1e-03) 0.49396070681427046, 0.007079160062184253
RCAL Readout Calibration	Confusion
(0,)	P(0 \| 0) = 0.992 P(1 \| 1) = 0.989 Confusion Matrix: Key: labels: (0, 1, 2, 3, 4) protocol: RCAL
(1,)	P(0 \| 0) = 0.990 P(1 \| 1) = 0.990 Confusion Matrix: Key: labels: (0, 1, 2, 3, 4) protocol: RCAL
(2,)	P(0 \| 0) = 0.991 P(1 \| 1) = 0.988 Confusion Matrix: Key: labels: (0, 1, 2, 3, 4) protocol: RCAL
(3,)	P(0 \| 0) = 0.992 P(1 \| 1) = 0.988 Confusion Matrix: Key: labels: (0, 1, 2, 3, 4) protocol: RCAL
(4,)	P(0 \| 0) = 0.989 P(1 \| 1) = 0.990 Confusion Matrix: Key: labels: (0, 1, 2, 3, 4) protocol: RCAL

NOX on Qudits

The make_nox() function extends to higher-dimensional qudits without any modifications. To see this, we consider the analogy of the above GHZ state preparation circuit for qutrits.

[9]:

# set the register dimension to 3 (i.e. qutrits)
tq.settings.set_dim(3)

# make a noisy simulator
sim = tq.Simulator().add_depolarizing(0.01, match=tqs.GateMatch(tq.Gate.cx3))

# create the circuit
circuit = tq.Circuit(
    [
        {(0): tq.Gate.f3},
        {(0, 1): tq.Gate.cx3},
        {(0, 2): tq.Gate.cx3},
        {(0, 3): tq.Gate.cx3},
    ]
)
circuit.measure_all()

# generate the NOX circuits
circuits = tq.make_nox(circuit)

# run the simulation
sim.run(circuits, n_shots=500)

# set which observables and outcomes to estimate
labels = ((0, 1, 2, 3),)
observables = ["W01W01W01W01", "1111", "0000", "2222", "0120"]

# fit
estimate_collection = circuits.fit(labels, observables=observables)
estimate_collection

[9]:

True-Q formatting will not be loaded without trusting this notebook or rerunning the affected cells. Notebooks can be marked as trusted by clicking "File -> Trust Notebook".

NOX Noiseless Output Extrapolation	Circuit #0 Labels (0, 1, 2, 3) Key: labels: (0, 1, 2, 3) measurement_basis: W01W01W01W01 mitigation: ('NOX',) n_marked: 3 protocol: RC seq_label: 159974003 twirl: Paulis on [0, 1, 2, 3]
$ev_\texttt{2222}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	3.3e-01+0.0e+00j (7.3e-03) (0.3321333333333332+0j), 0.007261096673658574
$ev_\texttt{1111}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	3.2e-01+0.0e+00j (8.2e-03) (0.3222333333333333+0j), 0.008172097654618992
$ev_\texttt{0120}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	-3.3e-05+0.0e+00j (3.3e-05) (-3.3333333333333335e-05+0j), 3.3333333333333335e-05
$ev_\texttt{0000}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	3.3e-01+0.0e+00j (8.0e-03) (0.32593333333333324+0j), 0.008011189492710997
$ev_\texttt{W01W01W01W01}$ The expectation value of an output string, of a Pauli/Weyl observable, or of a mixed string.	-7.8e-03+2.4e-03j (1.8e-02) (-0.007750000000000248+0.0023960036171373315j), 0.017617484131578962

Download

Download this file as Jupyter notebook: nox_example.ipynb.